最も簡単な異常検知の手法 -ホテリングのT2理論

釣りっぽいタイトルで申し訳ないですが、多分事実です。
ホテリングの $T^{2}$ 理論 ¹ と呼ばれている手法を紹介します。元ネタは画像の本にあります。²

異常検知
問題設定と異常度の定義
Pythonによる実装
高次元の場合
Python による実装
まとめ

異常検知

例えば、何かの測定値からなるデータ $X$ があるとしましょう。人間が一人で長時間かけて、大量に計測したとします。これを聞いただけで、測定ミスがあるような気がします。そのようなデータから、変な値を見つけるのが異常検知です。³
今回の手法の適用範囲は、正規分布に従っているデータに限られます。しかし、無垢な測定値は大体正規分布に従うので、殆どのデータに使用できます。

問題設定と異常度の定義

ある正規分布から生成された大量のデータ $X$ があるとします。データ $X$ から変なデータが無い状態にするのが目標です。
ホテリングの $T^{2}$ 理論では、次に示す計算で異常値を見つけます。

[ホテリングの $T^{2}$ 理論の計算]

最尤推定で、平均値 $μ$ と分散 $σ^{2}$ を推定する。
全てのデータ $x$ に対して $F$ 統計量
$\begin{array}{r} α_{x} = {(\frac{x - μ}{σ})}^{2} \end{array}$
を計算する。自由度1の $χ$ 二乗分布で近似できるとする。
各データに対して、
$\begin{array}{r} I_{x} = \int_{α_{x}}^{\infty} χ^{2} d u \end{array}$
を計算する。
0.05未満か判定する。0.05未満なら異常値。 ⁴

手順3. で出てきた $α_{x}$ をデータxの異常度と呼びます。推定した確率分布の中で、xがどのくらいレアなサンプルなのかを測る量です。レアなデータは異常な値として捨てよう、というのが手順4.です。
理屈の話は別の記事で書くとして、具体的な計算をpython で実装しましょう。カイ二乗分布の5%点を求める方法で、異常かどうか判断しています。davisデータ(男女の体重・身長の対のデータ) にある、身長と体重を逆に入力したデータを見つけます。

Pythonによる実装

記事で使っているソースコードはgithub に置いてあります。
https://github.com/msamunetogetoge

Davis データの体重の記録データのみを使います。データ全体のヒストグラムを見てみます。

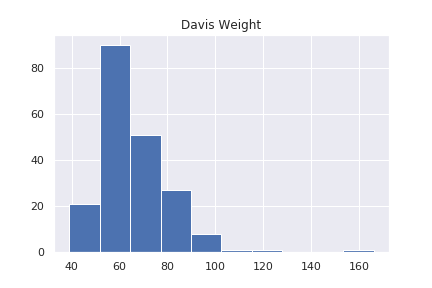
160 の辺りにデータがあります。力士かもしれませんが、外国のデータなので、打ち間違えでしょう。ホテリングの $T^{2}$ 理論で変なデータを見つけます。


mu = np.mean(x)
N=len(x)
sig =(np.sum( (x-mu)**2 ))/N
sig = np.sqrt(sig)

a = ( (x- mu)/sig )**2
import scipy.stats as stats
a_th =stats.chi2.ppf(q=0.95, df=1)
print(a_th)
#3.841458820694124

plt.plot(a)
plt.plot(a_th*np.ones(len(a)), c="r")
plt.title("Anomaly Of Dates")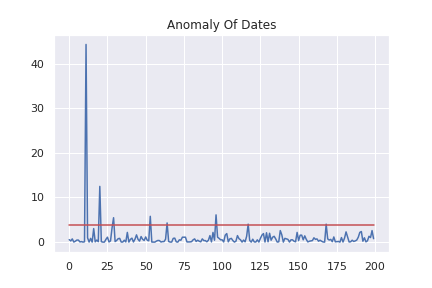

縦軸に $α_{x}$ を取って各データの異常度をプロットしています。赤線より上にあるデータが異常値と判断されます。
異常だと判断されたデータを見てみましょう。


anomaly = x[a>a_th].index
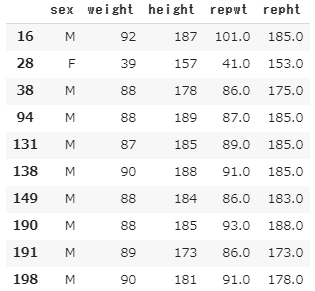
X.loc[anomaly]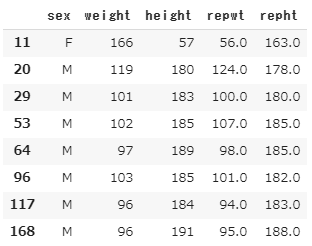

repwt , repht は再測定したデータです。
11のデータは、体重166 , 身長57 と明らかに変な値になっています。実際、再測定では、大体順序が逆になったような測定値になっているので、記入ミスが起きていたと考えられます。
他の異常と判断されているデータは肥満の人たちですね。データのヒストグラムの、大きい値の裾野の人たちです。
ホテリングの $T^{2}$ 理論は、実際には異常値が一つもなくても必ず異常値があるという判定を下すので、完全に鵜呑みにするのは微妙です。⁵
異常と判定されたデータを取り除いてもう一度ホテリングの $T^{2}$ 理論を適用してみましょう。


X = X.drop(index= anomaly)
x = X["weight"]
x.hist()
plt.title("Remove Anomaly Datas")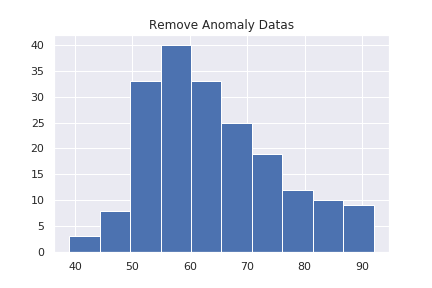

使っているデータの平均値が60くらいにあるので、40くらいにあるデータと、90付近にあるデータが異常と判定されそうです。

mu = np.mean(x)
N=len(x)
sig =(np.sum( (x-mu)**2 ))/N
sig = np.sqrt(sig)

a = ( (x- mu)/sig )**2
anomaly = x[a>a_th].index
X.loc[anomaly]

予想通りに異常判定されました。
データの素性が分かっている時に、変なデータを取り除きたい時には有用な手法です。

高次元の場合

身の回りでは、特徴量が1つだけのデータより、2,3 個の特徴量からなるデータが多いのではないでしょうか。その場合にも異常検知が出来ます。
今回の場合で言うと、身長と体重両方を見て、異常なデータを見つける事が出来ます。身長、体重両方のデータを見てみましょう。

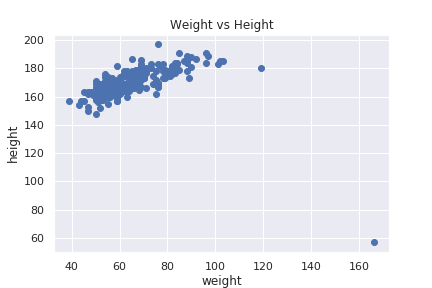
明らかに変なデータがありますが、先ほど異常と判定した身長と体重を逆に記録しているデータです。
データが多次元正規分布からサンプルされていると仮定することで、同じような事が出来ます。
特徴量の数はM個とします。つまり、各データは $x = (x_{1}, \dots, x_{M})$ と書けます。

[ホテリングの $T^{2}$ 理論(高次元)の計算]

最尤推定で、平均値 $μ$ と分散行列 $Σ$ を推定する。
全てのデータ $x$ に対して
$\begin{array}{r} α_{x} = (x - μ)^{T} Σ^{- 1} (x - μ) \end{array}$
を計算する。⁶自由度Mの $χ$ 二乗分布で近似できるとする。
各データに対して、異常度
$\begin{array}{r} I_{x} = \int_{α_{x}}^{\infty} χ^{2} (M) d u \end{array}$
を計算する。
0.05未満か判定する。0.05未満なら異常値。 ⁷

ホテリングの $T^{2}$ 理論と言いながら、そのような量が出てきませんが、
$\begin{array}{r} T^{2} = \frac{N - M}{(N + 1) M} (x - μ)^{T} Σ^{- 1} (x - μ) \end{array}$
をホテリングの $T^{2}$ 統計量と呼びます。これがF分布に従って、 $N >> M$ の時にカイ二乗分布で近似できる、と言うのがホテリングの $T^{2}$ 理論です。理論の詳細な計算は別の記事で書くと思います。
python で異常なデータを見つけてみましょう。

Python による実装

実装自体は、1次元の時と殆ど同じです。


x= X[["weight", "height"]]

mu = np.mean(x)
N=len(x)
M=len(x.columns)
Sig = np.dot((x-mu).T,(x-mu) )/N

import scipy.stats as stats
a_th =stats.chi2.ppf(q=0.95, df=M)
print(a_th)
#5.991464547107979

plt.plot(a)
plt.plot(a_th*np.ones(len(x)),c="r")
plt.title("Anomaly Score of 2-features Data")
plt.xlabel("Data Number")
plt.ylabel("Anomaly")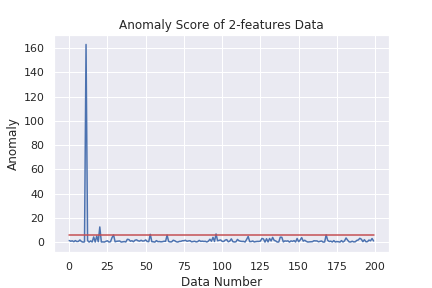

1次元の時と同じようなグラフが描けました。目で見るのが難しいデータを、目で見える形で評価できるので非常に有用です。
ぱっとデータクレンジングしたい時には、使うのがありかもしれません。

まとめ

異常検知の紹介をした
ホテリングの $T^{2}$ 理論の計算をpython で実装した。
グラフを描いて、異常値を見つけた。

統計学を勉強すると勝手に知ってる気もしますが。
この本で初めて機械学習と、Rに触れました。数学の詳細と、Rのコードを載せてくれているので、おすすめです。
応用範囲は測定データに限りませんが。
現れる $χ$ 二乗分布の5%点を求めておいて、 $α$ と比べても良いです。
データの近似分布の95%点を境に異常と判断しているので。
マハラノビス距離と呼ばれるやつです。確率分布から、データがどれくらい離れているかの目安になります。分散を考慮した、データの分布からの距離と言うイメージです。別の記事で詳しく書くかもしれません。
現れる $χ$ 二乗分布の5%点を求めておいて、 $α$ と比べた方が楽です。