K-means をpythonで実装する記事です。irisデータをクラスタリングします。
記事で使っているソースコードはgithub に置いてあります。
https://github.com/msamunetogetoge
K-means法
K-mean 法はクラスタリングの手法の一つです。
クラスタの中心を求め、それとデータとの距離を計算し、データを分類する情報を備えたクラスタリング行列を作成します。
クラスタの中心と、クラスタリング行列は、損失関数を最小化する事で作成します。
損失関数は、以下のように定義されます。
$$\begin{eqnarray}
J&=& \sum_{k=1}^K \sum_{n=1}^N r_{nk}\| x_n – \mu _k \| ^2
\end{eqnarray}$$
損失関数に出てくる\(r_{nk } \)がクラスタリング行列の成分です。1 \(r_{nk} \)は、\(x_n \)が属するクラスタ\(k_n \)と\(k \)が一致する時のみ、1をとり、それ以外では0とします。
実際は以下の手順で計算を行います。データは\(x_n \)で表します。2
- \( \mu _k \)を適当に与える
- nを固定して\( J_{nk} = \| x_n -\mu _k \| ^2 \)を計算し、\(J_{nk} \)が最小となる\(k=k_n \)を求める。これを各nに対して行う。
- \( r_{nk} = \delta _{nk_n } \)とする。
- Jを\( \mu _k\)について最小化する。
- Jを記録し、1回目の計算なら2に戻る。
- Jが収束していれば終了。収束していなければ2に戻る。
k-meansの原理の解説記事があるので、詳しくはそちらをどうぞ。

irisデータの確認
irisデータを使ってK-meansを動かします。目標を確認するために、データを見ておきます。
import numpy as np
np.random.seed(1)
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
from sklearn.datasets import load_iris
iris = load_iris()
X=pd.DataFrame(iris.data, columns=iris.feature_names)
sepal width とpetal length を軸に取って、あやめがどう分類されるか見てみます。
x1="sepal width (cm)"
x2 ="petal length (cm)"
for k in range(3):
X_0=X[y==k]
sns.scatterplot(x=x1,y=x2,data=X_0,label="label {}".format(k))
plt.legend()
plt.savefig("iris_classify.png")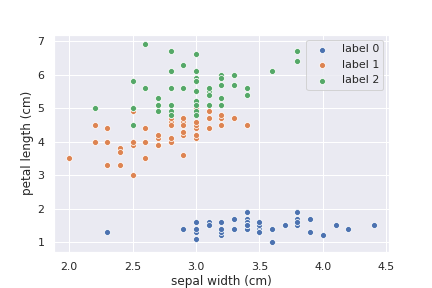
これと同じようなグラフが描ければ分類が成功しているといえます。
K-meansの実装
K-means では、データの分類を行うためのクラスタリング行列\(r_{nk} \)と、クラスタの中心\( \mu _k \)を作る事で、クラスタリングを行います。初めは適当に行列を生成し、そこからクラスタの中心を計算します。
K=3
K_n = np.zeros((len(X),K))
for i in range(len(X)):
a=np.random.randint(0,K)
K_n[i,a]=1
mu=(np.dot(X.T, K_n)/np.sum(K_n, axis=0)).T\( K_n \)が\(r_{nk} \)を表しています。\( \mu _k \)については、損失関数\(J\)を最小化するために、以下の計算を行っています。3
$$\begin{eqnarray}
J&=& \sum_{k=1}^K \sum_{n=1}^N r_{nk}\| x_n – \mu _k \| ^2 \\
\mu _k &=& \frac{\sum_{n=1}^N r_{nk} x_n }{\sum_{n=1}^N r_{nk}}
\end{eqnarray}$$
\( r_{nk} \)と\( \mu _k \)が得られたので、損失関数Jを計算し、最適なクラスタリング行列を求めます。以下のように計算していきます。
- (データ数,クラスタ数)次元の損失関数行列を作る。(i,k)成分\(J_{ik} \)は以下の通り。
$$\begin{eqnarray}
J_{ik} = \| x_i – \mu _k \| ^2
\end{eqnarray}$$ - 行列の\(i\)行を見て、損失関数を最小にする\(k_i \)を\(x_i \)のクラスタ番号とする。つまり、クラスタリング行列のi行目の\( (i,k_i ) \)成分だけを1にする。
- 更新したクラスタリング行列でクラスタの平均を計算する。
- 必要なら2と3を繰り返し計算する。
2と3の計算を実装します。
N=len(X)
J=np.zeros((N, K)) #損失関数行列の初期化
K_n = np.zeros((N, K)) #クラスタリング行列の初期化
for i in range(N):
for k in range(K):
J[i,k]=np.linalg.norm(X.iloc[i,:]-mu[k,:])**2 #損失関数行列の成分の計算
k_n=np.argmin(J[i,:])
K_n[i,k_n]=1 #クラスタリング行列の更新
mu=(np.dot(X.T, K_n)/np.sum(K_n,axis=0)).T #クラスタの平均を計算これを何度か計算すると、クラスタリングが出来ます。4
結果を以下に示します。
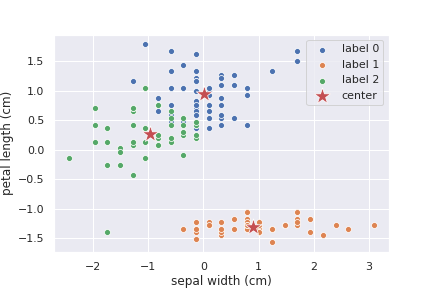
元の画像と比べると、かなり良い感じに計算出来ているのでは無いでしょうか。クラスタの中心も、確かにクラスタの中心っぽい場所になっています。
詳しいコードについては、githubを参照してください。別のデータにも使えるように、クラスの形でまとめています。
まとめ
- k-means の手法を確認した
- irisデータを見た
- k-means をpython で実装した

