統計学でも機械学習でも、必須の手法が最尤法です。尤度を最大にするのが最尤法ですが、案外教科書でも変な説明をしていたりします。
この記事では、尤度と最尤法について説明します。
得られたデータを活用したい
このご時世、データドリブンという言葉が横行しています。
何かを判断する時はデータを参考にしましょうと言うものです。取りあえずデータを集めたは良いものの、上手く扱えないという事も多いかと思います。機械学習が大いに流行っていますが、殆どの場合は機械学習無しで終わります。
データが数学的にどんな素性を持つか調べたい時に良くやる手法の一つに、データがある確率分布からサンプリングされているとする手法があります。つまり、どんなデータがどのくらいの確率で得られるのかを決めてしまおう、という事です。
ひとたび確率分布を作ってしまえば、どのような状況が有り得ないのか簡単に予測する事が出来ます。この手法を行う為に、最尤法が使われることが多いです。
最尤法とは、尤度を最大化する手法です。
意味不明だと思うので、説明していきます。
尤度とは?
尤度について説明します。
尤度は、データを確率分布からサンプリングしたものだと仮定した時の、確率の値の事です。つまり、以下のような値の事です。
データを\(X=\{x_1 , \cdots , x_n \} \)とし、\( x_i \)達はそれぞれ確率分布\(p(-|\theta ) \)から独立にサンプリングされたものと仮定します。この時、
$$\begin{eqnarray}
p(X|\theta ) = \prod_{i} p(x_i |\theta )
\end{eqnarray}$$
を尤度と呼びます。確率分布は、0から1までの値を取りますが、0に近ければ稀な事象を表し、1に近ければ良くある事象を表すと考える事が出来ます。
尤度は、仮定した確率分布でどれくらい現実のデータを近似出来ているかを測る指標となります。尤度が大きければ大きい程、確率分布が現実を近似出来ているという事になります。1
確率分布は、積の形になっていたり、\( \exp(f(x)) \)の形をしている事が多いので、扱いやすいように対数を取った対数尤度が考えられます。
$$\begin{eqnarray}
\log p(X| \theta ) =\sum \log p(x_i |\theta )
\end{eqnarray}$$
例として、適当にデータを生成して、尤度を計算してみます。
平均=10,分散=2の正規分布から データを生成し、ヒストグラムにします。次に、正規分布のパラメーターを変えてヒストグラムと一緒にグラフを描きます。
ヒストグラムの形と、分布の形が似ている方が尤度が大きくなるはずです。
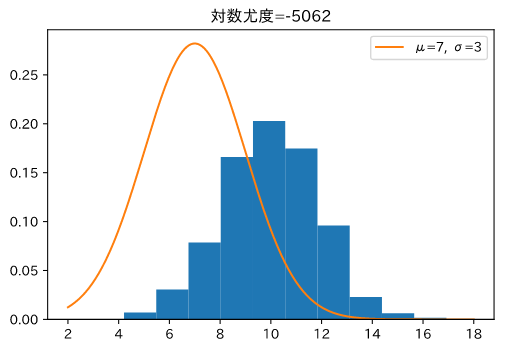
尤度小 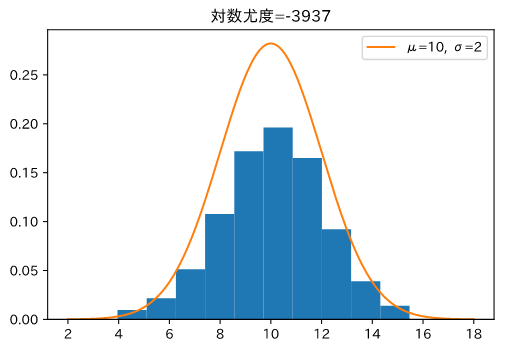
尤度大
ヒストグラムが生成したデータで、オレンジの線が正規分布をプロットしたものです。
2
オレンジ線とヒストグラムの形が同じ、右側の画像の方が尤度が大きくなっています。
最尤法とは?
最尤法とは、尤度を最大化する手法です。尤度が大きいという事は、仮定した確率分布がデータを良く表しているという事なので、自然な発想の手法です。尤度の代わりに、対数尤度を最大化する場合もあります。3
確率分布の値は1以下なので、\( \log \)を取ると必ず負の値を取ります。対数尤度はいつも負の値を取るわけですが、それを嫌って負の対数尤度を最小化する場合もあります。
この記事では、正の対数尤度を最大化するスタンスで行きます。
最尤法を行う場合は、確率分布の大元自体は固定することが多いです。4
尤度が最大になるパラメーターを求めるのが、最尤法である。とも言い換えられます。
最尤法を行うには
最尤法で何をするべきかは分かりましたが、何をすれば良いかははっきりしません。
尤度がいつも2次関数のような簡単な関数なら良いですが、確率分布は複雑な関数であることが多いです。
適当には最大値を求める事は出来ません。
そこで、関数の微分に注目します。ある点で、微分係数が正なら、その方向に向かっていけば関数の値は増大するのでした。逆もまた然りです。つまり、微分係数\(\alpha \)を使って
$$\begin{eqnarray}
x\rightarrow x+\alpha
\end{eqnarray}$$
とする事で、関数を常に大きく出来ます。
これは変数が沢山あっても同じす。以下の手順で最大の尤度を求める事が出来ます。5
[ステップ1]
適当なパラメーター\( \theta \)と学習率\( \eta \)を決める。
[ステップ2]
勾配\(\alpha = \nabla _{\theta} \log p(X|\theta ) \)を計算する。
[ステップ3]
パラメーター\( \theta \)を以下の式で更新する。
$$\begin{eqnarray}
\theta _{new} =\theta + \eta * \alpha
\end{eqnarray}$$
[ステップ4]
新しいパラメーターで尤度を計算する。
尤度が大きくなっていればステップ2に戻る。
尤度が殆ど変化していなければ、パラメーターを決定する。
蒸気の手法を勾配法と呼びます。機械学習の分野でも良く使われる手法です。尤度が殆ど変化していない、というのを判断するのは人間がやる必要があります。例えば、変化率が1%を下回ったら終了する、とか、指定回数は更新する、とかで行います。
また、解析的に勾配が計算できるときは、勾配=0 を計算してパラメーターを決定する事もあります。
最尤法の使用例
最尤法を使用する例をいくつかあげたいと思います。具体的な計算は、以下の記事で紹介しているので、興味があれば読んでみてください。

直接的に使用する場合と、手法の中に組み込まれている場合を紹介します。
データを確率分布で近似する場合
何かデータがある時に、データの値を新たにサンプリングしたり、塊から外れているデータがどのくらいあり得ない値なのか計算するために、データを簡単な確率分布で近似する事があります。
簡単な例として、平均値が分かっている正規分布(平均値=0)から生成したデータを使って、最尤法から分散を推定してみます。pythonのコードと結果を載せます。
import numpy as np
import matplotlib.pyplot as plt
from numpy.random import *
def Norm(x,mu,sig):
p=1/np.sqrt(np.pi * sig **2)*np.exp(-(x-mu)**2 /(2*sig**2))
return p
y=normal(loc=0,scale=5,size=100) #予測したいデータ, σ=5
X=np.linspace(-10,10,100) #予測に使うデータ
#勾配の計算
def gradient_scalar(f,x):
h=1e-4
x_1=np.copy(x)
x_1=x_1 + h
diff= (f(x_1) - f(x))/h
return diff
#勾配法のコード
def Learning(f,x,eta):
grads=gradient_scalar(f,x)
params=np.array([])
likelyfood=np.array([])
for i in range(10000):
x_1=np.copy(x)
LF_old=f(x)
grads=gradient_scalar(f,x_1)
x=x_1+eta*grads
params=np.append(params,x)
LF=f(x)
likelyfood=np.append(LF,likelyfood)
return params, likelyfood
mu=0
func=lambda sigma:np.sum(np.log(Norm(X,mu,sigma)))$勾配を計算するための関数の定義
params,lf=Learning(func,2,0.001)

勾配法で分散を求めると、5.8くらいに収束しています。上手く求める事が出来ませんでしたが、これは理論的に仕方ない事です。詳しい話は以下の記事でしています。

回帰分析の係数を最尤法で決定する。
(単)回帰分析は、
$$\begin{eqnarray}
y=ax+b+\epsilon
\end{eqnarray}$$
という関係を仮定して、データを表す手法です。\(\epsilon \)が確率分布6 からサンプリングされていると仮定する事で、最尤法を使ってパラメーター\(a ,b\)を推定する事が出来ます。
まとめ
- 尤度の説明をした。
- 最尤法の説明をした。
- 簡単な問題で、最尤法の計算をコード付きで解説した。


