見せかけの相関に注意しましょう。
データを弄ると必ず聞く言葉です。
偏相関係数を見ましょう。
時々聞く言葉です。というわけで偏相関係数の説明をします。
偏相関係数は、共通の特徴量を持つと思われる量の相関を測るものです。
相関係数が高いのに偏相関係数が低い状態の事を、見せかけの相関がある状態という訳です。
相関係数の復習から始めて、偏相関係数の定義を学んで、時系列分析での応用を説明します。
最後に、pythonで計算させてみます。
参考文献は2冊です。
記事で使っているソースコードはgithub に置いてあります。
https://github.com/msamunetogetoge
相関係数
相関係数の定義を復習します。
期待値を取る操作を\(E[-] \)で表すとき1 、\( x , y \)の相関係数\(r_{x,y} \)は,色々な量を定義して、以下のように計算されます。
$$\begin{eqnarray}
{\rm Cov } (x,y) &=& E[(x-E[x]) (y-E[y] )]\\
{ \rm Var} (x) &=& { \rm Cov } (x,x) =E[x^2] – \left( E[x] \right) ^2 \\
r_{x,y} &=&\frac{ {\rm Cov } (x,y) } {\sqrt{ { \rm Var} (x) { \rm Var} (y)}}
\end{eqnarray}$$
\(x \cdot y = {\rm Cov } (x,y) \)を内積だと思うと、相関係数は\(x \)と\(y \)のなす角度を測っていると解釈できます。そうすると、\( \| r_{x,y} \| \)が1に近いという事は、\( x, y\)が似ていると解釈できます。
耳にタコが出来るほど聞く話ですが、相関係数が高いからと言って、\(x, y \)の間に因果関係があるとは限らない事に注意が必要です。
例えば、体重と年収が相関があったとしましょう。体重が重い程、年収が高いようなデータがあったとします。意味不明だなと思って調べてみると、何故かデータ収集の対象年齢が12歳からとなっていることが分かりました。12歳の子供は体重が軽く、年収がほぼ0なので、そんなデータになっていたと分かってめでたしめでたしです。
未知の事象に挑戦している時に、同じような事が起きたときに冷静に行動するための量として、偏相関係数があります。
偏相関係数
偏相関係数は、\( x,y,z, z_1 ,\cdots , z_n \)というデータがあるとき、\(x , y \)から、\(z \)たちの影響を除いた相関係数です。この意味を説明します。
\(x , y \)から、\(z \)たちの影響を除いた 偏相関係数\(r_{x,y,z}\)は以下のように定義されます。
\(x, y \) を\(z \)たちから回帰した量を \(\hat {x} , \hat{y} \)とします。
$$\begin{eqnarray}
y’ &=& y- \hat{y}\\
z’ &=& z- \hat{z} \\
r_{x,y,z} &=&\frac{ {\rm Cov } (x’,y’) } {\sqrt{ { \rm Var} (x’) { \rm Var} (y’)}}
\end{eqnarray}$$
変数が大量にある場合でも同じ定義です。\(\hat{y} -y \)を行う事で、\(y \)から\(x\) の影響を排除していると考えます。
実際、\(y’ ,x \)は無相関である事が示せます。単回帰の場合に計算してみます。
単回帰の時、回帰式は以下のようになっていました。
2
$$\begin{eqnarray}
\hat{y} &=& \hat{a_y} x + \hat{b_y}\\
\hat{a_y} &=&\frac{ {\rm Cov } (x,y) } { {\rm Var } (x)} = r_{x,y} \\
\hat{b_y} &=& E[y] – \hat{a_y} E[x]
\end{eqnarray}$$
これらの式を元に共分散を計算します。
$$\begin{eqnarray}
{\rm Cov } (x, y’ ) &=& E[(x-E[x] )(y’-0)]\\
&=& E[ (x-E[x]) \{ (y- E[y] )-r_{x,y} (x-E[x]) \} ] \\
&=& {\rm Cov } (x,y) – r_{x,y} E[(x- E[x])^2 ] \\
&=& {\rm Cov } (x,y) – {\rm Cov } (x,y) =0
\end{eqnarray}$$
\( r_{x,y,z} \)を計算してみます。
まずは\( x , y\)が\(z \)だけに依っていると仮定した場合3です。
$$\begin{eqnarray}
r_{x,y,z} &=& \frac{ {\rm Cov } (x’,y’) } {\sqrt{ { \rm Var} (x’) { \rm Var} (y’)}} \\
&=& \frac{ E[x’ y’ ] } {\sqrt{E[x’ ^2 ] E[y’ ^2] } }
\end{eqnarray}$$
\( E[x’ y’ ] , E[x’ ^2 ] \)を計算すると以下のようになります。
$$\begin{eqnarray}
E[x’ y’] &=& (r_{x,y}- r_{x,z}r_{y,z}){\rm Var }(x) {\rm Var }(y) \\
E[x’ ] &=& {\rm Var }(x) ^2 (1- r_{x,z} ^2)
\end{eqnarray}$$
偏相関係数の式に代入すると、
$$\begin{eqnarray}
r_{x,y,z} = \frac{ r_{x,y}- r_{x,z}r_{y,z} }{\sqrt{1-r_{x,z} ^2} \sqrt{1- r_{y,z} ^2 } }
\end{eqnarray}$$
です。
\(x, y \)が\(z_1 , \cdots , z_n \)に依る場合も少しだけ計算しておきます4 。回帰式を$$\begin{eqnarray}
\hat{y} = \beta _0 + \sum_{i=1}^n \beta_{i} z_{i}
\end{eqnarray}$$
と書く時、\( \beta \)たちは、
$$\begin{eqnarray}
\beta = (z^T z )^{-1} (z^T y)
\end{eqnarray}$$
と書けます。ただし、\(z \)は\( (1, z_1 , \cdots , z_{n } ) \)と\(1 \)と\(z_i \)たちを横に並べて得られる (データ数)\( \times (n+1) \) 行列です。また、以下のようにも書けます。
\(z\)の分散共分散行列\(S\)と、\(y\)と \(z_i \)たちの共分散\(S_y \)は、以下のように計算出来ます。
$$\begin{eqnarray}
S_{i,j} &=&{\rm Cov} (z_i , z_j ) \\
{S_{y}} _i &=& {\rm Cov} (y , z_i )
\end{eqnarray}$$
この行列と、 \( \beta _0 = -E[y]+\sum \beta _i E[z_{i}]\)で、 \(\beta_1 , \cdots , \beta _n \)は、
$$\begin{eqnarray}
\beta = S^{-1} S_y
\end{eqnarray}$$
となります。行列とベクトルで書くと、回帰式は
$$\begin{eqnarray}
\hat{y} = z S^{-1} S_y
\end{eqnarray}$$
となります。偏相関係数は、この回帰式を使って
$$\begin{eqnarray}
r_{x,y,z_1 , \cdots , z_n} = \frac{ {\rm Cov } (x’,y’) } {\sqrt{ { \rm Var} (x’) { \rm Var} (y’)}}
\end{eqnarray}$$
と書かれます。手計算するのは大変ですが、データがある場合にパソコンに計算させるのは簡単です。
時系列分析での応用
偏相関係数は時系列分析で重要な役割を果たします。具体的には、定常なAR過程か否かを見極めるのに使う事が出来ます。つまり、定常な\(AR(p) \)過程 なら、 ある次数から\(p+1 \)から偏相関係数が0 となります。5
簡単の為に、\(AR(1) \)過程の2次の偏相関係数を計算してみます。\( \{ y_t \} \)を定常な \(AR (1) \)過程とします。
$$\begin{eqnarray}
y_t = \phi y_{t-1} + \epsilon _t
\end{eqnarray}$$
ただし、\(\{ \epsilon _t \} \)は分散0のホワイトノイズとします。
2次の偏相関係数を計算するために、\( y_{t-1} \)による\( y_t , y_{t-2} \) の回帰式を考えます。6
$$\begin{eqnarray}
\hat{y}_{t-2} = \beta y_{t-1}
\end{eqnarray}$$
最小二乗法から、\(\beta =\phi \)が分かります。\(y_{t} \)についても同様です。このことから、
$$\begin{eqnarray}
r_2 &=& {\rm Cov} (y_{t-2} – \hat{y}_{t-2} , y_{t} – \hat{y}_{t} ) \\
&=& {\rm Cov} ( y_{t-2} – \phi y_{t-1} , \phi y_{t-1} +\epsilon _t – \phi y_{t-1} ) \\
&=& {\rm Cov} ( y_{t-2} – \phi y_{t-1} , \epsilon _t) =0
\end{eqnarray}$$
同じような計算で、3次以上でも0になることが分かります。
pythonでの計算
初めに、irisデータで偏相関係数を計算してみます。
patal length とpatal width の相関が非常に高いので、他の変数の影響を取り除いて偏相関係数を計算してみます。
from sklearn.datasets import load_iris
import pandas as pd
import numpy as np
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
X=df.iloc[:,:2]
X["beta_0"]=1
X=X[["beta_0","sepal length (cm)","sepal width (cm)" ]]
#patal length とpatal width の相関が0.96なので、偏相関係数を計算
y=df[["petal length (cm)","petal width (cm)"]]
beta = np.dot(np.dot(np.linalg.inv( np.dot(X.T , X) ) , X.T), y)
#重回帰による予測値
y_hat = np.dot(X, beta)
#patal length とpatal width の相関が0.96
Y = y - y_hat
S_Y =np.zeros((2,2))
for j in [0,1]:
Y_j =Y.iloc[:,j] - np.mean(Y.iloc[:,j])
for i in [0,1] :
Y_i =Y.iloc[:,i] - np.mean(Y.iloc[:,i])
S_Y[j,i]=np.dot(Y_i, Y_j)
pac = S_Y[0,1]/np.sqrt(S_Y[0,0]*S_Y[1,1])
print(pac)
#0.870769773836145偏相関係数は0.87 と大きな値になりました。
次に、適当に\(AR(1) \)過程を生成して相関係数と偏相関係数を計算してみます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
#相関係数計算の関数
def autcor(X, k):
X_bar = np.mean(X)
X_bar_k = X_bar * np.ones(k)
X_k = np.append(X_bar_k ,X)
k_X = np.append(X, X_bar_k )
r= np.dot(X_k -X_bar , k_X - X_bar )
r/= np.linalg.norm(X-X_bar)**2
return r
#偏相関係数計算の関数
def Pac(Y,k):
Y = pd.DataFrame(Y, columns=["y_t"])
for i in range(k):
if i ==0:
Y["y_t-1"] = Y["y_t"].shift().fillna(0)
else:
Y["y_t-"+str(i+1)]=Y["y_t-"+str(i)].shift().fillna(0)
X =Y.iloc[:,1:k-1]
y=Y.iloc[:,[0,k]]
beta = np.dot(np.dot(np.linalg.inv( np.dot(X.T , X) ) , X.T), y)
y_hat = np.dot(X, beta)
y_til = y - y_hat
S_Y =np.zeros((2,2))
for j in [0,1]:
Y_j =y_til.iloc[:,j] - np.mean(y_til.iloc[:,j])
for i in [0,1] :
Y_i =y_til.iloc[:,i] - np.mean(y_til.iloc[:,i])
S_Y[j,i]=np.dot(Y_i, Y_j)
pac = S_Y[0,1]/np.sqrt(S_Y[0,0]*S_Y[1,1])
return pac
#AR(1)の生成
phi = 0.6
epsilon = np.random.randn(200000)
T=1000
Y=np.zeros(T)
for t in range(T):
Y[t]=phi*Y[t-1] +epsilon[t]
#10次まで計算
n=10
pac=[]
ac=[]
for k in range(n):
pac=np.append(pac,Pac(Y,k+1))
ac = np.append(ac,autcor(Y,k+1))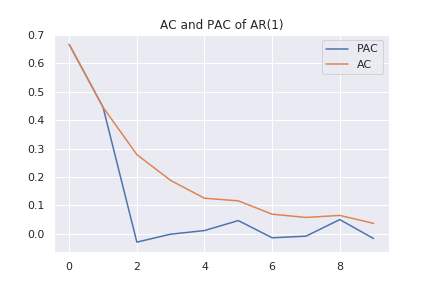
AR過程では、指数関数的に相関係数が小さくなっていく様子が見えます。また、偏相関係数は、2次以降でほぼ0となっています。MA過程では次のようなグラフになります。
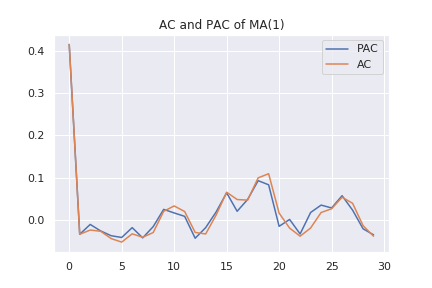
上の2つの図から分かるように、偏相関係数は、AR過程か否かを判定する材料には出来ますが、MA過程にはあまり効果がありません。
まとめ
- 相関係数について復習した
- 偏相関係数の定義を確認した
- 時系列分析における偏相関係数の役割を解説した
- python で計算してみた
- \(x \)が長さ\(n\)の、 データからなるベクトルだったら、\(E[x] =\sum_{i=1}^n x_i /n \)です。\( p(x) \)に従う確率変数なら\( E[x] = \int xp(x) dx \)です
- 計算は単回帰分析の記事を読んでください 。
- 単回帰の場合です。
- 省略されている計算は重回帰分析の記事に書いてます。
- 定常な\(MA(q) \)過程 なら、 相関係数が次数\(q+1 \)から0でした。MA過程に関する記事を読んでみて下さい。
- 一般にk次の偏相関係数を計算するための回帰係数について、\(\beta _{i} = \beta_{k-i} \)が成り立ちます。


