カイ二乗分布の性質 (世界一詳しく解説)

機械学習を先に学んでしまうと、カイ二乗分布が良く出てくる理由が分からないかもしれません。そこで、機械学習(ベイズ統計)では良く使うガンマ分布の一つとして定式化しておいて、カイ二乗分布の大事さ、特に標準正規分布との関係を見ていきます。
参考文献は一応2冊あります。

Bitly

Bitly

モーメント母関数と特性関数
ガンマ分布とカイ二乗分布
標準正規分布とカイ二乗分布
不偏分散とカイ二乗分布
多変量正規分布とカイ二乗分布
まとめ

モーメント母関数と特性関数

初めに、話をスムーズにするためにモーメント母関数と特性関数を定義しておきます。
Xが確率変数で、どの確率分布を考えているか明らかな時、$X $の期待値を$E[X] $で表します。モーメント母関数とは、次の量を指します。
$$\begin{eqnarray}
M_{X} (t) = E[ \exp (Xt ) ]
\end{eqnarray}$$
モーメント母関数の名前の由来は、モーメント母関数から全ての次数のモーメントが得られる事から来ています。¹
例えば、正規分布$ \mathcal{N}( \mu , \sigma ^2 ) $のモーメント母関数は、
$$\begin{eqnarray}
M_{X} (t) = \exp (\mu t + \sigma ^2 t^2 /2 )
\end{eqnarray}$$
です。一般に、モーメント母関数は存在するとは限りませんが、以下で定義する、特性関数はいつも存在します。
$$\begin{eqnarray}
\phi _{X} (t) = E[ \exp (iXt ) ]
\end{eqnarray}$$
フーリエ変換、逆変換の関係から、特性関数と確率分布は1対1に対応します。また、存在すれば、特性関数とモーメント母関数の間には以下の関係があるので、モーメント母関数からも確率分布は確定します。
$$\begin{eqnarray}
\phi _{X} (t) = M_X (it)
\end{eqnarray}$$
このことから、確率分布の性質を議論する上で、楽が出来る事があります。例えば、正規分布では
$$\begin{eqnarray}
\mathcal{N} (\mu _1 , \sigma _1 ^2 ) + \mathcal{N} (\mu _2 , \sigma _2 ^2 )
=\mathcal{N} (\mu _1 + \mu _2 , \sigma _1 ^2 +\sigma _2^2)
\end{eqnarray}$$
が成り立ちますが、モーメント母関数を使うと楽になります。
独立な確率変数を$ X \sim \mathcal{N} (\mu _1 , \sigma _1 ^2 ) , Y\sim \mathcal{N} (\mu _2 , \sigma _2 ^2 ) $として、
$Z=X+Y \sim \mathcal{N} (\mu _1 + \mu _2 , \sigma _1 ^2 +\sigma _2^2) $が成り立つ事を確かめます。
$$\begin{eqnarray}
M_{Z} (t) &=& E[ \exp (Zt )] \\
&=& E[ \exp (Xt)] E[ \exp (Yt)] \\
&=& \exp(\mu _1 t + \sigma _1 ^2 t^2 /2 ) \exp(\mu _2 t + \sigma _2 ^2 t^2 /2) \\
&=& \exp( (\mu _1 + \mu _2 )t + (\sigma _1 ^2 +\sigma _2^2 ) t^2 /2 )
\end{eqnarray}$$
これは、正規分布 $ \mathcal{N} (\mu _1 + \mu _2 , \sigma _1 ^2 +\sigma _2^2) $ のモーメント母関数です。

ガンマ分布とカイ二乗分布

ガンマ分布とカイ二乗分布について簡単な性質を計算してみます。ガンマ分布は、以下のような分布でした。色々な計算をまとめた記事があるので、計算はそちらを見てください。
$$\begin{eqnarray}
{ \rm Gam } (x| \alpha , \beta ) = \frac{1}{\Gamma (\alpha )} \frac{1}{\beta} \left( \frac{x}{\beta} \right)^{\alpha -1 } e^{-x/ \beta }
\end{eqnarray}$$

ガンマ分布のモーメントと母関数や、期待値、分散を書いておきます。
$$\begin{eqnarray}
M_x (t) &=& (1- \beta t )^{-\alpha} \\
E[X] &=& \alpha \beta \\
Var[X] &=& \alpha \beta ^2
\end{eqnarray}$$
モーメント母関数の形から分かるように、独立なガンマ分布にも、ある種の再生性があります。
$$\begin{eqnarray}
{ \rm Gam } ( \alpha _1 , \beta ) + { \rm Gam } ( \alpha _2, \beta ) = { \rm Gam } (\alpha _1 + \alpha _2 , \beta )
\end{eqnarray}$$
一応計算しておきましょう。$ X \sim { \rm Gam } ( \alpha _1 , \beta ), Y \sim { \rm Gam } ( \alpha _2 , \beta ) $で、XとYは独立とします。
$$\begin{eqnarray}
E[\exp((X+Y)t)] &=& E[\exp(Xt)] E[\exp(Yt)] \\
&=&(1-\beta t)^{-\alpha _1} (1-\beta t)^{-\alpha _2} \\
&=& (1-\beta t)^{-( \alpha _1 + \alpha _2 )}
\end{eqnarray}$$
最後の式は、
$ { \rm Gam } (\alpha _1 + \alpha _2 , \beta ) $のモーメント母関数なので、欲しい結論が得られました。

ガンマ分布の特別な場合をカイ二乗分布と呼びます。

$ { \rm Gam } (x| n/2, 2 ) $を自由度n のカイ二乗分布と呼び、$ \chi _n ^2 $で表す。

カイ二乗分布の確率分布や、モーメント母関数などを表すと、以下のようになります。
$$\begin{eqnarray}
\chi _n ^2　&=& \frac{1}{\Gamma (n/2)} \frac{1}{2} \left( \frac{x}{2} \right)^{n/2-1 } e^{-x/ 2 } \\
M_x (t) &=& (1- 2t )^{-n/2} \\
E[X] &=& n\\
Var[X] &=& 2n
\end{eqnarray}$$
ガンマ分布なので、カイ二乗分布の間でも再生性があります。
$$\begin{eqnarray}
\chi _n ^2 + \chi _m ^2 = \chi _{n+m} ^2
\end{eqnarray}$$
わざわざ名前が付いている分布なので、大事な分布なのですが、そのことを見ていきます。

標準正規分布とカイ二乗分布

カイ二乗分布が登場するシチュエーションを見てみます。

$Z \sim \mathcal{N}(0,1) $のとき、$Z^2 $は $\chi ^2 _1 $に従う。

標準正規分布があれば、カイ二乗分布があるのです。一応計算しておきます。
モーメント母関数を計算して、$ \chi _1 ^2 $が出てくることを確かめます。
$$\begin{eqnarray}
M_{Z^2} (t)&=& E[ e^{z^2 t } ]\\
&=& \frac{1}{\sqrt{2\pi }} \int dz e^{z^2 t } e^{-z^2 /2} dz \\
&=& \frac{1}{\sqrt{2\pi }} \int dz \exp(- \frac{1-2t}{2} z^2 ) dz \\
&=& \frac{1}{\sqrt{2\pi }} \frac{1}{\sqrt{1-2t}} \int dz \exp(\frac{-x^2}{2} ) dx \\
&=& (1-2t)^{-1/2}
\end{eqnarray}$$
途中で、$x= (1-2t)z $と変数変換しました。
最後の式は$ \chi _1 ^2 $のモーメント母関数なので、$ Z^2 $が自由度1のカイ二乗分布に従う事が分かりました。
上の主張と、自由度の足し算が出来るということから、次の事が分かります。

$Z_1 , \cdots , Z_n \sim \mathcal{N}(0,1) $がそれぞれ独立なとき、$\sum Z_i ^2 $は $\chi ^2 _n $に従う。

実際に標準正規分布からのサンプルを二乗して足したものをヒストグラムに描いてみると、カイ二乗分布とほぼ一致することが確かめられます。

np.random.seed(0)
z=np.zeros([10,100])
for i in range(10):
    z[i]=np.random.randn(100)
chi_ = np.sum(z**2, axis=0)

chi = np.random.chisquare(10,100)

sns.distplot(chi_,label="10個の標準正規分布から")
sns.distplot(chi,label="自由度10カイ二乗分布から")
plt.title("分布の比較")
plt.legend()
plt.savefig("chi_from_norms.png")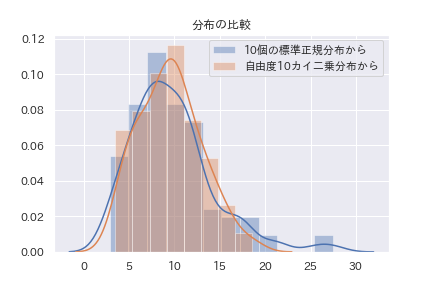

さらに大事な事として、正規分布からサンプリングして、不偏分散を考えるとカイ二乗分布が出てくるという話があります。

不偏分散とカイ二乗分布

$ X_1 , \cdots , X_n \sim \mathcal{N}(\mu ,\sigma ^2 ) $とする。また、それぞれの変数は独立とする。$Z_i =( X_i – \bar{X} )/\sigma $とする。ただし、$ \bar{X} $は$X_i $ 達の標本平均で、$\bar{X} =\sum X_i /n $を表す。
このとき、
$$\begin{eqnarray}
\sum_{i=1} ^n (Z_i -\bar{Z} )^2 \sim \chi _{n-1} ^2
\end{eqnarray}$$
が成り立つ。²
さらに、 $\bar{Z} $と $ \sum_{i=1} ^n (Z_i -\bar{Z} )^2 $は独立。

上の主張のキモは、自由度がnでなくて、n-1 になるという事です。
$ \sum_{i=1} ^n (Z_i -\bar{Z} )^2 = \sum Z_i ^2 -n \bar{Z} ^2 $であり、$ Z_i , \sqrt{n} \bar{Z} $は標準正規分布に従いますが、$ n \bar{Z} ^2 $が$Z_i ^2 $達の自由度を奪っています。これは証明が面倒なので、大体の流れだけを書いておきます。
正確な証明は、参考文献を読んでください。

[証明の概略]
$ Z_i $などが標準正規分布になる事は、モーメント母関数を計算すれば分かる。
$ Z_1 , \cdots , Z_n , \bar{Z} $の組で考えると、どれが独立かはっきりしないので、直交変換$H $で、$ ( Z_1 , \cdots , Z_n ) \mapsto ( Y_1 =\sqrt{ \bar{Z}} , Y_2 , \cdots , Y_n ) $となるようなものを作る。³
これが作れると、
$$\begin{eqnarray}
\sum_{i=1} ^n (Z_i -\bar{Z} )^2 &=& \sum Z_i ^2 -n \bar{Z} ^2 \\
&=& Z^T Z – Y_1 ^2 \\
&=& (HY)^T HY -Y_1 ^2 \\
&=& \sum _{i=2} ^n Y_i ^2
\end{eqnarray}$$
となる。$Z_i $同士は独立で、標準正規分布に従い、$H $が直交変換なので、$Y_i $も標準正規分布に従う。
最後に、$Y_1 , \cdots , Y_n $は全て独立で、上の計算から、
$$\begin{eqnarray}
\sum _{i=2} ^n Y_i ^2 &=& \sum_{i=1} ^n (Z_i -\bar{Z} )^2 \\
Y_1 &=& \sqrt{n} \hat{Z}
\end{eqnarray}$$
なので、$\bar{Z} $と $ \sum_{i=1} ^n (Z_i -\bar{Z} )^2 $は独立。

実際に、統計量
$$\begin{eqnarray}
(n-1) Var(X) / \sigma ^2
\end{eqnarray}$$
を作ってヒストグラムにしてみると、カイ二乗分布とほぼ一致することが確認できます。

#データの準備 10種類の正規分布から100組のデータを集める
sample=10
size=100
sig=2
mu=1
x=np.zeros((size,sample))
for i in range(sample):
    np.random.seed(i)  
    x[:,i]=np.random.normal(loc=mu,scale=sig,size=size)
#統計量の計算とカイ二乗分布の準備
chi_=[]
for j in range(size):
    v=np.sum( (x[j,:] - np.mean(x[j,:]))**2)/(sample-1)
    V = (sample-1)*v/sig**2
    chi_.append(V)

chi = np.random.chisquare(9,100)
#グラフを描く
sns.distplot(chi_,label="10個の正規分布から")
sns.distplot(chi,label="自由度9カイ二乗分布から")
plt.title("分布の比較")
plt.legend()
plt.savefig("chi_from_norms2.png")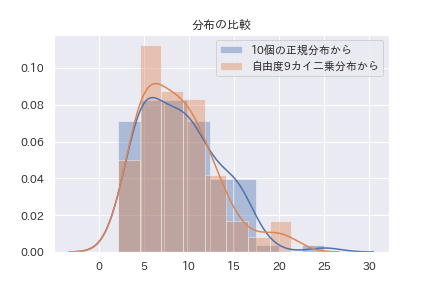

このような背景があるので、色々な場所でカイ二乗分布が出てくるわけです。
しかし、いきなり正規分布が得られている事は少ないので、近似的に正規分布が得られて、その結果カイ二乗分布が出てくる、という状況の方が多いかもしれません。
そのような状況の記事は別に書きたいと思います。

多変量正規分布とカイ二乗分布

標準正規分布に従う確率変数$X_1 , \cdots , X_n \sim \mathcal{N}(0,1) $があるとき、自由度nのカイ二乗分布が出て来ました。
$$\begin{eqnarray}
\sum_{i=1} ^n X_i ^n \sim \chi _n ^2
\end{eqnarray}$$
これらを、確率変数からなるベクトルだと思うと、以下のように書き直すことが出来ます。
$$\begin{eqnarray}
X &=& ( X_1 , \cdots , X_n ) \\
X^T X &=& \sum_{i=1} ^n X_i ^n \sim \chi _n ^2
\end{eqnarray}$$
多変量正規分布の話では、確率変数ベクトルの成分の共分散が0なら、成分は独立です。
つまり、$ X\sim \mathcal{N} ( 0, I_n ) $なら、
$$\begin{eqnarray}
X_i &\sim & \mathcal{N} (0,1) \\
X^T X &=& \sum_{i=1} ^n X_i ^2 \sim \chi _n ^2
\end{eqnarray}$$
という事です。
一変数の場合のように、標準多変量正規分布からカイ二乗分布が出て来ます。

$X =(X_1 , \cdots , X_n ) \sim \mathcal{N} (\mu , \Sigma ) $ とします。Xを標準化すると、自由度nのカイ二乗分布が得られます。⁴
$$\begin{eqnarray}
(X-\mu) ^T \Sigma ^{-1} (X- \mu ) \sim \chi _{n} ^2
\end{eqnarray}$$

これを証明するには、以下の事実を使います。⁵
$$\begin{eqnarray}
X & \sim & \mathcal{N} (\mu , \Sigma ) \\
AX+b & \sim & \mathcal{N} ( A\mu + b, A\Sigma A^T )
\end{eqnarray}$$
上の事実を認めると、
$$\begin{eqnarray}
X- \mu & \sim & \mathcal{N} ( 0, \Sigma )
\end{eqnarray}$$
です。なので、$ X \sim \mathcal{N} ( 0, \Sigma ) $ に対して、
$$\begin{eqnarray}
A\Sigma A^T &=& I \\
X^TA^T AX &=& X^T \Sigma ^{-1} X
\end{eqnarray}$$
となるような$A $が存在する事を示せば、$ AX \sim \mathcal{N} ( 0, A\Sigma A^T ) =\mathcal{N} ( 0, I) $となり、主張が示せます。
正規分布に使われる共分散行列が、正定値かつ対称としましょう。⁶
そうすると、$ \Sigma $は直交行列で対角化できます。
$$\begin{eqnarray}
H\Sigma H^T &=& \Lambda \\
H^T H&=&I
\end{eqnarray}$$
ただし、$ \Lambda =diag [ \lambda _1 , \cdots , \lambda _n $は固有値が対角に並んだ行列です。$ \Lambda _{\ast} = diag[ 1/\sqrt{\lambda _1} , \cdots ,1/\sqrt{\lambda _n} ] $とおいて、$ A= H\Lambda _{\ast} $としましょう。
$$\begin{eqnarray}
A\Sigma A^T = \Lambda _{\ast} ^2 \Lambda =I
\end{eqnarray}$$
であり、$\Sigma =H^T \Lambda H $なので、$ A^T A= \Sigma ^{-1} $が分かります。この事から
$$\begin{eqnarray}
X^TA^T AX &=& X^T \Sigma ^{-1} X
\end{eqnarray}$$
となります。これで、主張が示せました。
python で主張を確かめてみます。

#データの生成
np.random.seed(2)
sig=np.random.randint(1,10,5)
Sigma = np.dot(sig.reshape(-1,1), sig.reshape(1,-1)) + 1*np.eye(5)
mu =np.ones(5)
y=np.random.multivariate_normal(mean=mu ,cov=Sigma, size=100)
#
Y=np.array([])
for i in range(len(y)):
    chi_ = (y-mu)[i].reshape(-1,5)@ np.linalg.inv(Sigma)@(y-mu)[i].reshape(5,-1)
    Y=np.append(Y,chi_ )

chi = np.random.chisquare(5,100)
#グラフを描く
sns.distplot(Y,label="5次元正規分布から")
sns.distplot(chi,label="自由度5カイ二乗分布から")
plt.title("分布の比較")
plt.legend()
plt.savefig("chi_from_norm.png")

5次元正規分布→カイ二乗分布 — 5次元正規分布から自由度5のカイ二乗分布が出てくる

上の主張
$$\begin{eqnarray}
(X-\mu) ^T \Sigma ^{-1} (X- \mu ) \sim \chi _{n} ^2
\end{eqnarray}$$
は、変量正規分布を標準化するとカイ二乗分布が出てくるという意味ですが、一方で正規分布の肩に載っている量がカイ二乗分布になるという事でもあります。
$ (X-\mu) ^T \Sigma ^{-1} (X- \mu ) $は、$X $が正規分布$ \mathcal{N} (\mu , \Sigma ) $からの距離と捉える事も出来ます。⁷
この量を使って、異常検知のシステムを作る事が出来ます。
このことは別の記事で解説します。

まとめ

計算するためにモーメント母関数などを定義した
ガンマ分布の一つとしてカイ二乗分布を定義した
標準正規分布からカイ二乗分布を作った
分散からカイ二乗分布を作った
多変量正規分布からカイ二乗分布を作った。

$ E[X] , E[X^2 ] , \cdots , $を、1次,2次$ , \cdots $のモーメントと呼びますが、モーメント母関数を$X=0 $ でn階微分すれば、n次モーメントが得られます。
$ (n-1) Var(X) / \sigma ^2 \sim \chi _{n-1} ^2 $という事です。
Z=HY かつ、$H^T H=I $となるHを作ります。Helmert 行列というらしいです。
nは、ベクトルの成分の数です。
多変量正規分布の記事で証明してます。
正定値は、全ての固有値が0より大きいという事です。
マハラノビス距離と呼ばれます。