ベイズの定理を現実に近い設定で使ってみる記事です。初めに、事前分布などを決めて、計算をしてしまいます。次に、適当な設定で、ベイズの定理を使って予測してみます。
二項分布とベータ分布
今回の記事で使うのは二項分布とベータ分布です。
二項分布は、2種類の結果がある事象を複数回繰り返すような事象をモデル化するときに使われ、以下の表式になっています。
$$\begin{eqnarray}
f(x|\theta , n) = {}_n C _{x} \theta ^{x} (1-\theta )^{n-x}
\end{eqnarray}$$
ベータ分布は以下の表式です。
$$\begin{eqnarray}
{\rm Be }(y| \alpha , \beta ) =\frac{ y^{\alpha -1 } (1-y)^{\beta -1}}{\int_{0} ^{1} x^{\alpha -1 } (1-x)^{\beta -1} dx }
\end{eqnarray}$$
二項分布は、\(x \)に0位以上の整数しか入りませんが、 ベータ分布は実数値を入れる事が出来ます。また、ベータ分布の分母は、ベータ関数として知られています。また、ガンマ関数を用いて表す事が出来るので、計算上便利な性質を持っています。1
$$\begin{eqnarray}
{\rm Be }(\alpha, \beta ) &=& \frac{\Gamma (\alpha ) \Gamma (\beta ) }{\Gamma ( \alpha + \beta ) }\\
&=& \int_{0} ^{1} x^{\alpha -1 } (1-x)^{\beta -1} dx
\end{eqnarray}$$
ガンマ関数は、階乗の一般化だったことを思い出す2と、\(\alpha , \beta \)が自然数の時は、ベータ関数は簡単な形になります。
$$\begin{eqnarray}
{\rm Be }(y| \alpha , \beta ) =\frac{ \alpha ! \beta ! }{ ( \alpha +\beta )! }
\end{eqnarray}$$
ベイズの定理の計算
初めに、ベイズの定理を書いておきます。
$$\begin{eqnarray}
p(\theta |x ) = \frac{p(x|\theta ) p(\theta ) }{ p(x) }
\end{eqnarray}$$
\( p(\theta )= {\rm Be }(\theta | \alpha , \beta ) \)とし、 \( p(x|\theta ) \)を二項分布として計算しましょう。
計算で楽をするために、\( \log \)を取って計算します。
$$\begin{eqnarray}
\log p(\theta |x ) = (x+\alpha -1 ) \log x + (n-x+\beta -1 )\log(1-x) +{\rm const }
\end{eqnarray}$$
const は、\( \theta \)に関係ない項を表しています。
右辺が確率分布になっていると考えると、ベータ分布\( {\rm Be }(\theta |x+\alpha, n-x+\beta ) \)となっています。現実のモデルとして二項分布を使う時は、パラメーターの事前分布にベータ分布を使えば、事後分布もベータ分布という訳です。
$$\begin{eqnarray}
p(\theta |x ) = {\rm Be }(\theta | x+\alpha, n-x+\beta )
\end{eqnarray}$$
事後確率を最大にする\(\theta \)を求めておきましょう。この計算で求める\( \hat{\theta } \)が予測値になります。
\( \theta \)で微分して0とおき、\( \theta \)について解けば良いです。
$$\begin{eqnarray}
\frac{ \partial \log {\rm Be }(\theta | \alpha , \beta ) }{\partial \theta }
= \frac{\alpha -1 }{\theta} -\frac{\beta -1 }{1-\theta }
\end{eqnarray}$$
上の式を解いて、
$$\begin{eqnarray}
\hat{\theta } =\frac{\alpha -1 }{\alpha + \beta -1}
\end{eqnarray}$$
となります。
ベイズの定理の応用
これまでの計算を使って考えたいのは以下のような問題です。
人がいなくなってしまったので、良品/不良品を仕分けるロボットを導入した。購入する際には、識別率80%くたいですよと言われていたが、導入してみると、識別率は80%もないと感じた。数日分のデータを集めたので、識別率が80%あるのか調べる。
データを20個集めると、正しく識別しているのが15個、間違いが5個だったとしましょう。
ロボットが良品/不良品を識別するという事象を二項分布でモデル化し、\( \theta \)を求めましょう。3計算を楽にするために事前分布はベータ分布とします。また、購入した側としては、事前には何も知らないという事にしたいので、\( \alpha =\beta=1 \)として、一様分布にしましょう。
上の計算に当てはめると、\( n=20 , x=15 \)です。
つまり、事後分布は、
$$\begin{eqnarray}
p(\theta |n=20,x=15 ) = {\rm Be }(\theta | 15+1, 20-15+1 ) = {\rm Be }(\theta | 16, 6 )
\end{eqnarray}$$
です。ちなみに、確率分布を描くと以下のようになっています。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
from scipy import stats
!pip install japanize-matplotlib
import japanize_matplotlib
X=np.linspace(0,1,100)
beta = stats.beta.pdf(X,16,6)
plt.plot(X,beta,label="(α,β)=(16,6)")
plt.legend()
plt.title("ベータ分布")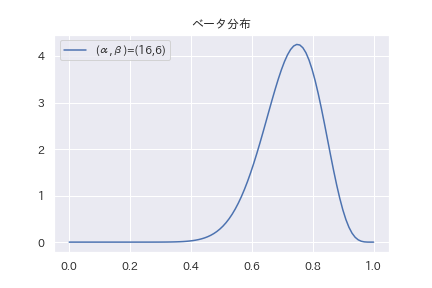
この時の識別率の推定値は
$$\begin{eqnarray}
\hat{ \theta} = \frac{15}{21}= 0.71
\end{eqnarray}$$
となります。また、\( \theta \)が0.8以上の確率は、事後分布を0.8から1まで積分する事で得られ、大体23%です。
theta = stats.beta.sf(0.8,16,6)
print(theta)
"""
0.2307041188518264
"""これらの事から、違和感は正しいと言えそうです。
今は事後分布として、\( {\rm Be }(\theta | 16, 6 ) \)が得られていますが、これを事前分布として、データを取得する事も出来ます。例えば、
新たに10個データを取得したとして、何個正しく識別すれば\( \hat{\theta } \)が0.8を超えるのか?
といった疑問に答える事も出来ます。この問題について考えてみましょう。
x個正しく識別できたとすると、事後分布は
$$\begin{eqnarray}
p(\theta |n=10,x ) = {\rm Be }(\theta | x+16, 10-x+6 ) = {\rm Be }(\theta | 16+x,16-x )
\end{eqnarray}$$
となります。この時、推定値\( \hat{\theta } \)は
$$\begin{eqnarray}
\hat{\theta } = \frac{15+x}{31}
\end{eqnarray}$$
です。これが0.8となるのは、
$$\begin{eqnarray}
x=9.8
\end{eqnarray}$$
の時です。実際、\(x=10 \)のとき、
$$\begin{eqnarray}
\hat{\theta } = 0.806
\end{eqnarray}$$
となり、推定値は0.8を超えます。10個のデータでは、挽回はかなり厳しいみたいですね。
このように、未来の出来事まで見据えた議論が出来るのがベイズ統計の良い所です。
補足
θの推定値を求めるなら、\( p(x| \theta ) \)の最尤推定をするという方法も考えられます。
二項分布で最尤推定すると、
$$\begin{eqnarray}
\hat{\theta } =\frac{x}{n}
\end{eqnarray}$$
となります。勿論この方法でも\( \theta \)を推定できますが、未来の予測をしようと思っても出来ません。また、\(\theta \)についての分布は持っていないので、\( \theta \)が\( \theta _0 \)以上となる確率などは求める事は出来ません。
問題によって、ベイズ的手法と、古典統計的手法は使い分ける必要があります。
まとめ
- 二項分布とベータ分布を紹介した
- ベイズの定理の計算をした
- 応用として、適当な状況を考えて計算した
- 最尤推定との比較をした
- ベイズの定理を使う時にはあまり必要ないですが。
- ガンマ分布の解説で計算しています。
- \( \theta \)が識別率です。

