ベイズの定理を使う時は、大体共役事前分布を用いて事後分布を計算します。その際に、確率分布の基本的な統計量を知っていると計算が楽になります。どんなデータにどんな確率分布を指定するべきかは、確率分布について馴染みが無いと見当も尽きません。そんな悩みを減らす為に、よく使われる確率分布のグラフを描いて、基本的な統計量を計算しておこうと思います。
扱っている確率分布[ベルヌーイ分布,二項分布,ポアソン分布,正規分布,多次元正規分布,ガンマ分布]
統計量の定義
確率分布\( p(x) \)があったとして、統計量を定義します。定義した統計量を計算1します。
[期待値]
確率\(p(x) \)の下での、関数\( f(x) \)期待値は,以下の式で定義される量です。
$$\begin{eqnarray}
E[f(x)] = \int f(x) p(x) dx
\end{eqnarray}$$
[平均値]
\(p(x) \)の平均値は,xの期待値です。つまり、以下の式です。
$$\begin{eqnarray}
E[x] = \int x p(x) dx
\end{eqnarray}$$
[分散]
\(p(x) \)の分散は,以下の式で定義される量です。
$$\begin{eqnarray}
V[p(x)] = E[x^2] -E[x]^2
\end{eqnarray}$$
[エントロピー]
\(p(x) \)のエントロピーは,以下の式で定義される量です。
$$\begin{eqnarray}
H[p(x)] = – E [\log p(x) ]
\end{eqnarray}$$
積分は、変数が定義された全ての領域で行います。また、離散的な確率分布の場合は、積分を和に変えて、変数の取りうる値全てで足し合わせます。
平均値は、得られる値の大体の値をを表しています。分散は、得られる値がばらつく範囲を表しています。エントロピーは、得られる値の予測のしにくさを表しています。
数種類の確率分布に対して、上の3つの量を計算し、グラフに描いてみます。
ベルヌーイ分布
ベルヌーイ分布は、離散的な値を取る確率分布で、2つの値しかとらない事象を扱う時に登場します。確率分布の定義は以下です。 \(x \in \{ 0,1 \} \)とします。
$$\begin{eqnarray}
Bern(x |\mu ) = \mu ^{x} (1-\mu ) ^{1-x}
\end{eqnarray}$$
\(\mu \)を変えてグラフを描くと以下のようになります。
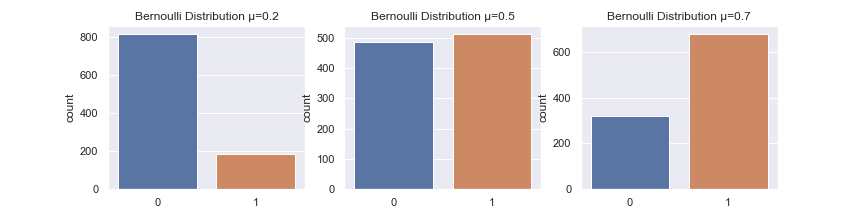
諸々の統計量を計算しましょう。
$$\begin{eqnarray}
E[x]= \sum x \mu ^{x} (1-\mu ) ^{1-x} =\mu \\
E[x^2]= \sum x^2 \mu ^{x} (1-\mu ) ^{1-x} =\mu
\end{eqnarray}$$
これらから、
[平均値]
$$\begin{eqnarray}
E[x] = \mu
\end{eqnarray}$$
[分散]
$$\begin{eqnarray}
V[p(x)] = E[x^2] -E[x]^2 =0
\end{eqnarray}$$
[エントロピー]
$$\begin{eqnarray}
H[p(x)] &=&- E [\log p(x) ] \\
&=&- \sum \left( x\log \mu +(1-x ) \log (1-\mu ) \right) \\
&=&-\mu \log \mu – (1-\mu ) \log (1-\mu )
\end{eqnarray}$$
このエントロピーは、交差エントロピーと呼ばれ、機械学習の誤差関数として利用されます。例えば、ロジスティック回帰で使われます。ロジスティック回帰についての記事はこちらをご覧ください。
https://masamunetogetoge.com/classification-logisticregression
二項分布
二項分布は、ベルヌーイ分布の拡張版です。ベルヌーイ分布に従う事象を何回か続ける時に使います。例えば、100回コインを投げて裏表を記録するとかです。確率分布の定義は以下です。 \(m \in \{ 0,\cdots , M \} \)とします。また、\( 0! =1 \)とします。
$$\begin{eqnarray}
Bin(m |M,\mu ) = {}_M C_m \mu ^{m} (1- \mu )^{M-m}
\end{eqnarray}$$
\( M=10 \) を固定して、\(\mu \)を変えてグラフを描いてみます。
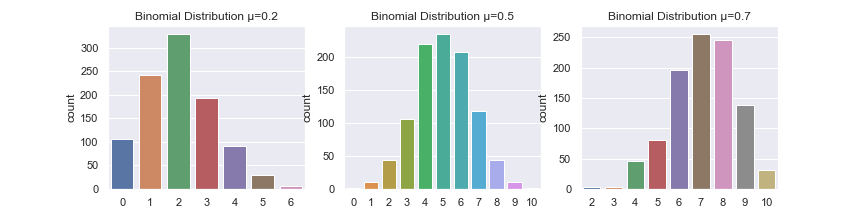
諸々の統計量を計算しましょう。
$$\begin{eqnarray}
E[m]&=& \sum m \binom{M}{m} \mu ^{m} (1- \mu )^{M-m} \\
&=& \sum M\mu \binom{M-1}{m-1} \mu ^{m-1} (1- \mu )^{M-m } \\
&=& M\mu
\end{eqnarray}$$
$$\begin{eqnarray}
E[m^2]&=& \sum m^2 \binom{M}{m} \mu ^{m} (1- \mu )^{M-m} \\
&=& \sum m(m-1) \binom{M}{m} \mu ^{m} (1- \mu )^{M-m} \\
&+& \sum m \binom{M}{m} \mu ^{m} (1- \mu )^{M-m} \\
&=& \mu ^2 M(M-1) + M\mu \\
&=& M \mu \left( (M-1) \mu +1 \right)
\end{eqnarray}$$
ただし、二項係数に関する以下の公式を使いました。下の式で、mを\(m(m-1) \)に変えても、同じような式が成り立ちますが、それも使います。
$$\begin{eqnarray}
m \binom{M}{m} =m\frac{M!} {(M-m)! m!} = M\frac{(M-1)!}{(M-m)!(m-1)!} =M \binom{M-1}{m-1}
\end{eqnarray}$$
上の計算を使って、諸々の量を計算しましょう。
[平均値]
$$\begin{eqnarray}
E[m] = M\mu
\end{eqnarray}$$
[分散]
$$\begin{eqnarray}
V[p(x)] &=& E[m ^2] -E[m]^2 = M \mu \left( (M-1) \mu +1 \right) -(M\mu )^2 \\
&=& M\mu (1-\mu)
\end{eqnarray}$$
[エントロピー]
\( E[\log m ] \)が必要ですが、綺麗な表式が見つからないので、計算しません。教えてください。
ポアソン分布
ポアソン分布は0以上の整数を作りたいときに使う確率分布です。定義は以下です。
$$\begin{eqnarray}
Poi(x| \lambda ) = \frac{\lambda ^x}{x! } e^{-\lambda}
\end{eqnarray}$$
ただし、\(\lambda \) は0より大きい実数です。\(\lambda \)を変えてグラフを描くと以下のようになります。 \( \lambda \)が大きくなると色々な数字が得られるようになります。
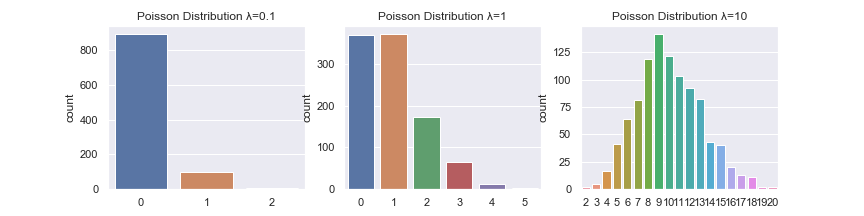
統計量を計算しましょう。
$$\begin{eqnarray}
E[x]&=& \sum_{x\geq 0} x \frac{\lambda ^x}{x! } e^{-\lambda} \\
&=& \lambda \sum _{x \geq 1} \frac{\lambda ^{x-1}}{(x-1)! } e^{-\lambda} \\
&=& \lambda \sum _{x \geq 0} \frac{\lambda ^{x}}{x! } e^{-\lambda} \\
&=& \lambda \\
E[x^2 ]&=& \sum_{x\geq 0} x^2 \frac{\lambda ^x}{x! } e^{-\lambda} \\
&=& \lambda \sum _{x \geq 1} x \frac{\lambda ^{x-1}}{(x-1)! } e^{-\lambda} \\
&=& \lambda \sum _{x \geq 0}(x+1) \frac{\lambda ^{x}}{x! } e^{-\lambda} \\
&=& \lambda ( \lambda +1 )
\end{eqnarray}$$
注意するのは、\( e^(ax) =\sum \frac{ (ax)^n }{n!} \)という事です。上の計算から平均値と分散を計算しましょう。
[平均値]
$$\begin{eqnarray}
E[x] = \lambda
\end{eqnarray}$$
[分散]
$$\begin{eqnarray}
V[p(x)] &=& E[x ^2] -E[x]^2 = \lambda
\end{eqnarray}$$
[エントロピー]
計算出来ると思いますけど出来たら載せます。
ポアソン分布は、平均と分散が一致するという面白い分布になっています。
正規分布
正規分布の平均値と分散は以下の記事で計算しているので、エントロピーだけ計算します。

正規分布は、連続な値を取る確率分布で、以下の式で定義されます。
$$\begin{eqnarray}
\mathcal{N}(x|\mu , \sigma ^2 ) =\frac{1}{\sqrt{2\pi \sigma ^2 }} \exp(-\frac{1}{2\sigma ^2} (x-\mu )^2
\end{eqnarray}$$
エントロピーの計算に使う期待値を書きます。
$$\begin{eqnarray}
E[x]&=& \mu
E[x^2]= \mu ^2 +\sigma ^2
\end{eqnarray}$$
[エントロピー]
$$\begin{eqnarray}
H[p(x)] &=&- E [\log p(x) ] \\
&=& \frac{1}{2} E\left[ \log 2\pi +\log \sigma ^2 + \frac{(x-\mu ) ^2}{\sigma ^2} \right] \\
&=& \frac{1}{2}(1 + \log 2\pi + \log \sigma ^2 )
\end{eqnarray}$$
多次元正規分布
多次元正規分布の平均値や分散は以下の記事で計算しています。エントロピーだけ計算しましょう。

多次元正規分布は以下の式で定義されます。出てくる変数は全てベクトルですが、手抜きで表式は数字と一緒です。
$$\begin{eqnarray}
p(x|\mu , \Sigma )=\frac{1}{\sqrt{ (2\pi )^{D} |\Sigma |}} \exp \left( -\frac{1}{2} (x -\mu )^{T} \Sigma^{-1}(x-\mu) \right)
\end{eqnarray}$$
エントロピーの計算に必要な量を書きます。
$$\begin{eqnarray}
E[x ]&=& \mu \\
E[x x^{T}] &=& \mu \mu^{T} +\Sigma
\end{eqnarray}$$
[エントロピー]
$$\begin{eqnarray}
H[p(x)] &=&- E [\log p(x) ]\\
&=& \frac{1}{2} E\left[ D\log 2\pi +\log |\Sigma | + (x-\mu )^{T} \Sigma^{-1} (x-\mu ) \right] \\
&=& \frac{1}{2}\left( D\log 2\pi + \log |\Sigma | +D \right)
\end{eqnarray}$$
\(E\left[ (x-\mu )^{T} \Sigma^{-1} (x-\mu ) \right] \)の計算は、数字も行列だという事と、行列のトレースに関する性質
$$\begin{eqnarray}
Tr(AB)=Tr(BA)
\end{eqnarray}$$
を使います。
エントロピーは、次元が大きくなるだけで増加するという結果を示しています。自由度が大きくなる分予測がしにくいという直感にあっています。
ガンマ分布
ガンマ分布は、正の実数を作りたいときに使う確率分布です。ポアソン分布の共役事前分布になっています。ガンマ分布は以下の式で定義されます。\( x ,a,b \)は0より大きい実数です。
$$\begin{eqnarray}
p(\lambda |a, b)&=& C(a,b) \lambda ^{a-1} e^{b\lambda}\\
C(a,b) &=& \frac{b^a}{\Gamma (a)}
\end{eqnarray}$$
ここで、\( \Gamma (a) \)はガンマ関数で、以下の式で定義されます。
$$\begin{eqnarray}
\Gamma (a) = \int_{0} ^{\infty} t^{a-1} e^{-t} dt
\end{eqnarray}$$
ガンマ関数のグラフを描いてみます。\( x=0 \)から\(x=1.5 \)くらいまでは単調減少で、それ以降は単調増加です。
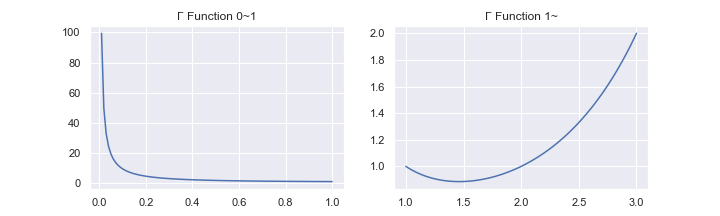
大事な性質として、次の性質2があります。証明は部分積分とかで出来ます。
$$\begin{eqnarray}
\Gamma (a+1) &=& a\Gamma (a) \\
\Gamma (1) &=& 1
\end{eqnarray}$$
\( a, b \)を変化させてガンマ分布のグラフを描いてみます。
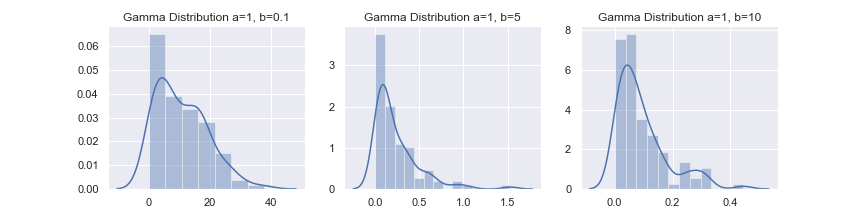
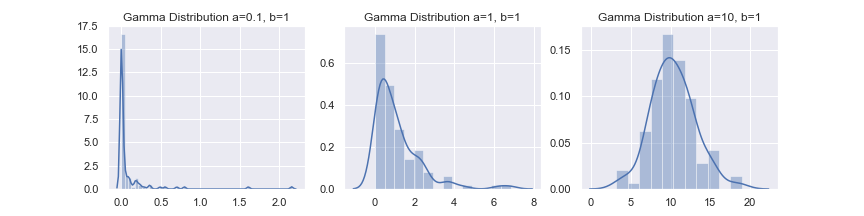
平均値や分散の計算に必要な量を計算しましょう。
$$\begin{eqnarray}
E[\lambda ] &=& \int C(a,b) \lambda ^{a} e^{-b\lambda } d\lambda \\
&=& C(a,b) \frac{1}{b^{a+1}} \int \lambda ^{a} e^{-\lambda } d\lambda \\
&=& C(a,b) \frac{1}{b^{a+1}} \Gamma (a+1) \\
&=&\frac{a}{b} \\
E[\lambda ^2 ] &=& \frac{a^2}{b^2}
\end{eqnarray}$$
\( E[\log \lambda ] \)を計算するために以下の量を導入します。
$$\begin{eqnarray}
\psi (x) &=& \frac{d} {dx} \log \Gamma (x) \\
&=& \frac{1}{\Gamma (x) }\int t^{x-1} e^{-t} \log t \ dt
\end{eqnarray}$$
\( \psi (x) \)をディガンマ関数と呼びます。グラフを描いてみましょう。不連続な点があります。
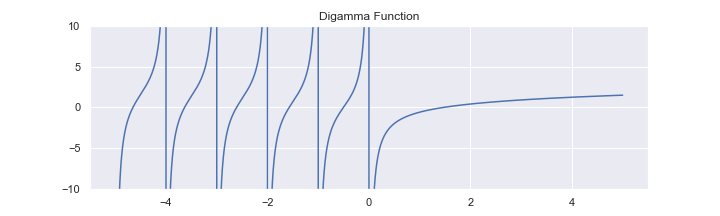
ディガンマ関数を用いて、 \( E[\log \lambda ] \) は以下のようになります。
$$\begin{eqnarray}
E[\log \lambda ] &=& \int C(a,b) \lambda ^{a-1} e^{-b\lambda }\log \lambda d\lambda \\
&=& \frac{1}{\Gamma (a) } \int \lambda ^{a-1} e^{-\lambda } (\log \lambda – \log b )d\lambda \\
&=& \psi (a) -\log b
\end{eqnarray}$$
これらで、統計量の計算をしましょう。
[平均値]
$$\begin{eqnarray}
E[\lambda] = \frac{a}{b}
\end{eqnarray}$$
[分散]
$$\begin{eqnarray}
V[p(\lambda)] = E[\lambda ^2] -E[\lambda ]^2 =0
\end{eqnarray}$$
[エントロピー]
$$\begin{eqnarray}
H[p(\lambda)] &=&- E [\log p(\lambda) ] \\
&=&- E\left[ \log C(a,b) +(a-1)\log \lambda -b \lambda \right] \\
&=&-E\left[ a\log b -\log \Gamma (a) +(a-1) \psi (a) -(a-1) \log b -a \right] \\
&=& \log \Gamma (a) -(a-1) \psi (a) -\log b +a
\end{eqnarray}$$
まとめ
・パラメーターによって、グラフの形ががらりと変わる確率分布もある。
・エントロピーは、次元が大きくなったり、分散が大きいと大きくなる傾向がある。


