EMアルゴリズムの一般化 | マサムネの部屋

EMアルゴリズムを一般的な形で書きます。何個かの確率分布に対して計算してみます。

一般化EMアルゴリズム
正規分布への応用
ベルヌーイ分布への応用
まとめ

一般化EMアルゴリズム

一般的な状況でEMアルゴリズムを考えます。目標は確率分布
$$\begin{eqnarray}
p(X| \theta )
\end{eqnarray}$$
のパラメーターたち$ \theta $を最尤法で決定する事です。
その為に、データの情報を持った隠れ変数$ Z $ が存在すると仮定します。¹$Z $は離散確率変数として、確率分布$q(Z) $に従うとしましょう。この時、対数尤度が以下のように分解できます。
$$\begin{eqnarray}
\log p(X| \theta ) &=& \mathcal{L}(q, \theta) +KL(q \| p)
\end{eqnarray} $$
ただし、$ \mathcal{L} (q, \theta ) , KL( q \| p)$²は以下の式で定義されます。
$$\begin{eqnarray}
\mathcal{L}(q, \theta) &=& \sum_{Z} q(Z) \log \left\{ \frac{p(X,Z| \theta )}{q(Z)} \right\} \\
KL(q \| p) &=& – \sum_{Z} q(Z) \log \left\{ \frac{p(Z|X,\theta)}{q(Z)} \right\}
\end{eqnarray} $$
この式 ³ から、一般化されたEMアルゴリズムを考える事が出来ます。KLダイバージェンスについての基本的な性質や、EMアルゴリズムについては以下の記事をどうぞ。

初めに、KL ダイバージェンスは0以上だったことに注意しましょう。つまり、$ \log p(X| \theta ) \geq \mathcal{L} (q, \theta ) $が成り立っています。以下の図の状態が常に成り立っているという訳です。

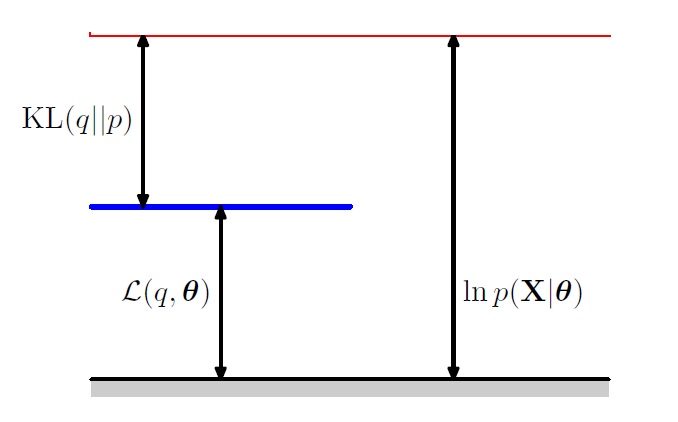
$ \log p(X| \theta ) $を最大化する$ \theta $を求めるのが目標でした。適当に$ \theta _{ {\rm old} } $ を固定したとしましょう。
KLダイバージェンスがの項で、$ KL( q\| p ) =0 $が成り立つのは、$ q=p $となる時で、その時に限ることを思い出しましょう。
つまり、$q = p(Z|X, \theta _{ {\rm old} } ) $の時です。 $q=p $とすることで、 $ \log p(X| \theta ) = \mathcal{L}( \theta ) $ となります。この時、対数尤度は$ \mathcal{L} $ を展開して、以下のようになります。
$$\begin{eqnarray}
\log p(X| \theta ) &=& \sum_{Z} p(Z|X, \theta _{ {\rm old} } ) \log \left\{ \frac{p(X,Z| \theta )}{q(Z)} \right\}
\end{eqnarray} $$
この状態で、$ \log p(X| \theta ) $ を最大化するために、式を整理します。
$$\begin{eqnarray}
\mathcal{L}( \theta ) &=& \sum_{Z} p(Z|X, \theta _{ {\rm old} } ) \log \left\{ \frac{p(X,Z| \theta )}{q(Z)} \right\} \\
&=& \sum_{Z} p(Z|X, \theta _{ {\rm old} } ) \log p(X,Z| \theta ) – H_q (p) \\
&=& \sum_{Z} p(Z|X, \theta _{ {\rm old} } ) \log p(X,Z| \theta ) + {\rm const }
\end{eqnarray} $$
1項目は $ Q(\theta , \theta _{\rm old} ) $ と書かれることがあります。2項目は、$ \theta $ を変数に持たないので、今のステップでは定数です。1項目は$ p_{\rm old} $で $ \log p(X,Z| \theta ) $の期待値を取っているのと同じなので、
$$\begin{eqnarray}
E_{p_{ \rm old}} [ \log p(X,Z| \theta ) ]
\end{eqnarray}$$
とも書けます。
この式を$ \theta $で微分して0 とおき、パラメーターを更新すると何が起きるでしょうか。
$ \theta $ を更新する前は、 $ \log p(X| \theta ) = \mathcal{L} +0 $となっていましたが、パラメーターを$ \theta _{\rm new} $に更新すると$ \log p(X| \theta ) $の値が大きくなります。また、 $ p_{\rm old } = p( Z|X, \theta _{ \rm old} ) $ と置くと、一般には$ KL( p_{\rm old } \| p( Z|X, \theta _{ \rm new} ) \neq 0 $ です。新しくなった式
$$\begin{eqnarray}
\log p(X| \theta ) &=& \mathcal{L}(p_{old}, \theta) +KL(p_{old} \| p)
\end{eqnarray} $$
に対して、今までの操作を繰り返すことで対数尤度を大きくすることが出来ます。この手順をまとめてEMアルゴリズムが導出出来ます。

[Eステップ]
1回目だけパラメーター$ \theta $を初期化する。
$$\begin{eqnarray}
{\rm arg} \max _{q(Z)} \mathcal{L}(q, \theta ) \Leftrightarrow KL(q\| p ) =0
\end{eqnarray}$$
つまり、$q = p(Z|X, \theta )$とする。また、
$$\begin{eqnarray}
Q(\theta , \theta _{\rm old} ) &=& E_{p_{ \rm old}(Z) } [ \log p(X,Z| \theta ) ] \\
p_{ \rm old}(Z) &=& p(Z|X, \theta _{ {\rm old} } )
\end{eqnarray}$$
を計算する。

[Mステップ]
$ \theta $で微分して、$ Q$を最大化するためのパラメーターを求める。つまり、
$$\begin{eqnarray}
{\rm arg} \max _{\theta } Q(\theta , \theta _{\rm old} )
\end{eqnarray}$$
を行う。

この一連の手順もEMアルゴリズムと呼びます。いくつかの確率分布に対してEMアルゴリズムを計算してみます。

正規分布への応用

確率分布が正規分布の場合に上記のEMアルゴリズムを考えましょう。パラメーターは$ \theta = \{\mu _k , \Sigma _k , \pi _k \} _{k=1, \cdots , K} $とします。
$$\begin{eqnarray}
p(x|\theta ) =\sum_{k} \pi _k \mathcal{N}(x| \mu _k , \Sigma _k )
\end{eqnarray}$$
として、隠れ変数$Z$ はカテゴリー分布に従うと仮定します。
$$\begin{eqnarray}
q(z| \pi ) = \prod {\pi _k} ^{z_k}
\end{eqnarray}$$
必要な分布を計算します。
$$\begin{eqnarray}
p(X,Z| \theta ) &=& \prod _{k} \prod_{n} \left[ \pi _k \mathcal{N}(x_n |\mu _k , \Sigma _k )\right] ^{z_{nk}}\\
\log p(X,Z| \theta ) &=&
\sum_k \sum_n z_{nk} ( \log \pi_k + \log \mathcal{N}(x_n |\mu _k , \Sigma _k ) )\\
p(Z|X, \theta ) &=&
\frac{\prod_{k} \prod_{n} \left[ \pi _k \mathcal{N}(x_n |\mu _k , \Sigma _k ) \right]^{z_{nk}} }
{ \sum_{Z} \prod_{k} \prod_{n} \left[ \pi _k \mathcal{N}(x_n |\mu _k , \Sigma _k ) \right]^{z_{nk}} }
\end{eqnarray}$$
次に、Mステップを行うための期待値$ Q(\theta , \theta _{\rm old} ) = E_{p_{ \rm old}(Z) } [ \log p(X,Z| \theta ) ] $の計算をしましょう。対数尤度$ \log p(X,Z| \theta ) $ の中で$Z $に関係あるのは$ \log $達の前に出ている$z_{nk} $だけです。
$ Z = \{ z_1 , \cdots , z_n \} $で、行列になっていますが、各成分毎に期待値を計算します。
$$\begin{eqnarray}
E_{p(Z|X,\theta )} [z_{nk} ] &=& \sum_{z_{n}} z_{nk} p(z_{nk} |x_{n} , \mu _k , \theta _k , \pi _k )
\end{eqnarray}$$
ここで、$ \sum_{z_n } $は、取り得る$ z_n $全てのパターンについて和を取るという意味です。つまり、$ z_{n} = \delta _{ni} , i=1, \cdots , K $の全ての場合を考えて和を取るということです。
$$\begin{eqnarray}
E_{p(Z|X,\theta )} [z_{nk} ] &=&
\frac{
\sum_{z_{n}} z_{nk} \prod _k \left[ \pi _k \mathcal{N} (x_n | \mu_k , \Sigma _k ) \right] ^{z_{nk} }
}{
\sum_{z_n } \prod _{k} \left[ \pi _k \mathcal{N}(x_n |\mu _k , \Sigma _k ) \right]^{z_{nk}}
} \\
&=& \frac{\pi _k \mathcal{N} (x_n |\mu _k , \Sigma _k ) } {\sum_k \pi _k \mathcal{N} (x_n |\mu _k , \Sigma _k ) }
\end{eqnarray}$$
分母、分子では$ z_{nk} =1 $となる部分以外は消えてしまう事を考えれば出てきます。
この期待値は、混合正規分布に対するEMアルゴリズムで導出した$ \gamma (z_{nk} ) $と一致します。以下の記事を見てください。

EMアルゴリズム

扱うデータが複数の分布を持っていそうな時、分布の混合割合と、パラメーターを推定する方法があります。それはEMアルゴリズムと呼ばれています。EMアルゴリズムの原理について解説します。

計算は既に行っているので、新しく更新するべきパラメーターの形だけ書きます。

結果を見やすくするために、次のように記号を準備します。
$$\begin{eqnarray}
E_{p(Z|X,\theta )} [z_{nk} ] &=& \gamma (z_{nk} )\\
N_k &=& \sum_n \gamma (z_{nk} ) \\
N&=& \sum_k N_k
\end{eqnarray}$$
とします。これらを使って、パラメーターの更新は以下のように行います。 $$\begin{eqnarray}
\mu _k &=& \frac{ \sum_{n} \gamma (z_{nk}) x_n }{N_k} \\
\Sigma _k &=&
\frac{1}{N_k} \sum_n \gamma (z_{nk} ) (x_n -\mu _k ) (x_n – \mu _k ) ^{T} \\
\pi_ k & =& \frac{N_k } {N}
\end{eqnarray}$$

混合正規分布に対するEMアルゴリズムの記事では、対数尤度を分解するという事はしていませんでしたが、やっている事は同じでした。次はベルヌーイ分布について計算してみます。

ベルヌーイ分布への応用

混合ベルヌーイ分布について、EMアルゴリズムを適用してみます。(D次元)ベルヌーイ分布は2択の状況を表現する確率分布で、パラメーター$ \mu \in (0,1 ) $と確率変数$ x \in \{ 0,1 \} $を用いて、以下の式で表されます。
$$\begin{eqnarray}
p(x| \mu ) =\prod_{i=1}^{D} \mu_{i} ^{x_i} (1-\mu_{i} )^{1-x_i }
\end{eqnarray}$$
例えば、白黒画像を考えます。白黒画像は、白い部分は 0 , 黒い部分は1を割り当てた行列で表現されます。$0 \sim 9 $の白黒画像を分類する、という問題では、10個のベルヌーイ分布が混合された状態が出てきます。データがK個にクラスタリングされた状況を考え、$x $ のクラスターを指定する隠れ変数を$ z $, 混合比率を$ \pi = \{ \pi _1 , \cdots , \pi _{K} \} $ として、以下の確率分布を考えます。
$$\begin{eqnarray}
p(x|\mu , \pi )&=& \sum _k \pi _k p(x|\mu _k ) \\
p(x|\mu _k ) &=& \prod \mu_{ki} ^{x_i} (1-\mu_{ki} )^{1-x_i } \\
p(x| z, \mu ) &=& \prod_{i=1}^{D} p(x|\mu _k ) \\
\end{eqnarray}$$
データが$X= \{ x_1 , \cdots , x_n \} $の時、EMアルゴリズムに必要な量を計算します。
$$\begin{eqnarray}
p(X,Z|\mu , \pi )&=&\prod_k \prod_n \left[ \pi _k p(x_n |\mu _k ) \right]^{z_{nk}} \\
p(Z|X, \mu , \pi )　&=& \sum_{Z} \prod_k \prod_n \left[ \pi _k p(x_n |\mu _k ) \right]^{z_{nk}}
\end{eqnarray}$$
$p(Z |X, \mu , \pi ) $ で、$ \log p(X,Z|\mu , \pi ) $の期待値を取るのですが、計算するべき量は$ E[z_{nk}] $であり、混合正規分布の時と同じ手法が使えます。
$$\begin{eqnarray}
\gamma _{z_{nk} } &=&E_{p(Z|X,\theta )} [z_{nk} ] \\
&=& \frac{\pi _k p(x_n |\mu _k ) } {\sum_k \pi _k p (x_n |\mu _k ) }
\end{eqnarray}$$
この量を用いて、$ Q( \theta , \theta _{\rm old} ) $とその微分は以下のように計算出来ます。

$$\begin{eqnarray}
Q( \theta , \theta_{\rm old} ) &=&
\sum_n \sum_k \gamma (z_{nk} ) \left\{ \log \pi _k + \sum_i x_{ni} \log \mu _{ki} +(1-x_{ni} )\log \mu _{ki} \right\}
\end{eqnarray} $$
式の見やすさの為に、以下の量を導入しておきます。
$$\begin{eqnarray}
N_{k} &=& \gamma (z_{nk} ) \\
\bar{x_k}&=& \frac{1}{N_k} \sum_{n} \gamma (z_{nk}) x_n
\end{eqnarray} $$
$ Q $の微分を計算します。
$$\begin{eqnarray}
\frac{\partial Q}{\partial \mu _{ki} } &=& \sum_{i} \frac{ N_k \mu _{ki} -\sum_n \gamma (z_{nk})x_{ni} } {\mu _{ki}(\mu _{ki} -1 )}
\end{eqnarray}$$
この式と混合正規分布のように、ラグランジュの未定乗数法を用いる事でパラメーターの更新式が分かります。
$$\begin{eqnarray}
\mu _k &=& \bar{x_k} \\
\pi _k &=& \frac{N_k }{N}
\end{eqnarray}$$
もちろん、$N =\sum _k N_k $です。