のっぴきならぬ事情により、python などで計算を行う事が出来ない人もいるかもしれません。そのような人の為に、エクセルだけで完結するコンテンツを作ります。
今回の記事では、ホテリングのT2理論によって、異常値を検出する処理をVBAで行います。
エクセルファイルやVBAファイルはgithubに置いておくので好きに使ってください。
https://github.com/msamunetogetoge
問題設定
日々蓄積されていくようなデータがあるとします。データはn次元で横ベクトルの形でまとまっているとします。1
データの中から、変なデータを見つけるのが目標です。
手法の特性上、1つのデータの次元が大きくなると、変なデータの判定が緩くなるので、見る必要が無い次元は積極的に削除した方が良いです。
ホテリングのT2理論
ホテリングのT2理論については、解説記事を書いているので、詳しい計算などはそちらをご覧ください。また、pythonでの実装も書いているので、エクセルにこだわる必要が無い人は、そちらを読んでみてください。
データが1次元(1列)の時のホテリングのT2理論は以下のように行います。
[ホテリングの\(T2\)理論の計算(1次元)]
- 最尤推定で、平均値\( \mu \) と分散 \( \sigma ^2 \)を推定する。
- 全てのデータ\(x \) に対して \( F\)統計量
$$\begin{eqnarray}
\alpha _x = \left( \frac{x-\mu }{\sigma } \right) ^2
\end{eqnarray}$$
を計算する 。\( \alpha _x \sim \chi _{1}^2 \) - 各データに対して、
$$\begin{eqnarray}
\int _{\alpha } ^{\infty} \chi ^{2} du =0.95
\end{eqnarray}$$
となる\( \alpha \)を求める。 - \( \alpha > \alpha _x \)なら、xは異常値と判断する。
データが2次元以上の時は、以下のように計算します。計算される量は、マハラノビス距離とも呼ばれています。
[ホテリングの\(T2\)理論の計算(多次元)]
- 最尤推定で、平均値\( \mu \) と分散 \( \Sigma \)を推定する。
- 全てのデータ\(x \) に対して
$$\begin{eqnarray}
\alpha _x = (x-\mu ) \Sigma ^{-1} (x-\mu) ^T
\end{eqnarray}$$
を計算する 。\( \alpha _x \sim \chi _{M}^2 \)とする。 - 各データに対して、
$$\begin{eqnarray}
\int _{\alpha } ^{\infty} \chi _{M} ^{2} du =0.95
\end{eqnarray}$$
となる\(\alpha \)を求める。 - \( \alpha > \alpha _x \)なら、xは異常値と判断する。
VBAで実装
VBAで上の計算を実装します。2
初めてVBAで処理を書いたので、VBAらしいコードかは分かりません。取りあえずコードの全文を載せ、要所の解説をします。大事、と言っている部分を変更すると、動作がおかしくなります。3
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
Sub Hotelling() '変数の定義 Dim LastRow, LastColumn Dim Data, Data_T, Sigma Dim ws0, ws1 As Worksheet 'worksheet の指定 Set ws0 = Worksheets("data") Set ws1 = Worksheets("result") 'resultシートに色を付けるので初期化する ws1.Cells.ClearFormats 'データの情報を取得する LastRow = ws0.Cells(Rows.Count, 1).End(xlUp).Row LastColumn = ws0.Cells(1, Columns.Count).End(xlToLeft).Column Data = ws0.Range(ws0.Cells(2, 2), ws0.Cells(LastRow, LastColumn)).Value Data_T = WorksheetFunction.Transpose(Data) Data_all = ws0.Range(ws0.Cells(1, 1), ws0.Cells(LastRow, LastColumn)).Value N = LastRow - 1 k = LastColumn - 1 D = Data '共分散の計算 ReDim h(k) For i = 1 To k S = 0 For j = 1 To N S = S + Data(j, i) Next j h(i) = S / N Next i root_N = N ^ (1 / 2) For i = 1 To k For j = 1 To N D(j, i) = (Data(j, i) - h(i)) / root_N Next j Next i D_T = WorksheetFunction.Transpose(D) Sigma = WorksheetFunction.MMult(D_T, D) Sigma_inv = WorksheetFunction.MInverse(Sigma) 'カイ二乗関連の計算と判定結果の記録 C = WorksheetFunction.MMult(WorksheetFunction.MMult(Data, Sigma_inv), Data_T) ReDim chi(N), test(N) chi_M = WorksheetFunction.ChiSq_Inv(0.95, k) For i = 1 To N chi(i) = C(i, i) If chi(i) < chi_M Then test(i) = "正常" Else test(i) = "異常" End If ws1.Cells(i + 1, 1) = test(i) If ws1.Cells(i + 1, 1) = "異常" Then ws1.Cells(i + 1, 1).Font.Color = RGB(255, 0, 0) End If Next i ws1.Cells(1, 1) = "test" 'resultシートにもデータの写しを作成する For i = 1 To N + 1 For j = 1 To k + 1 ws1.Cells(i, j + 1) = Data_all(i, j) Next j Next i End Sub |
初めのDim ~~は変数の定義です。必要かは良く分かりません。
次に、Set ~でワークシートの名前を指定しています。これは大事です。
|
1 2 3 4 5 6 |
Dim LastRow, LastColumn Dim Data, Data_T, S Dim ws0, ws1 As Worksheet 'worksheet の指定 Set ws0 = Worksheets("data") Set ws1 = Worksheets("result") |
次に、異常値を検出したら赤字を使いたいので、一度ワークシート内の文字の色の設定を初期化し、データの情報4 を取得しています。これも大事です。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
'resultシートに色を付けるので初期化する ws1.Cells.ClearFormats 'データの情報を取得する LastRow = ws0.Cells(Rows.Count, 1).End(xlUp).Row LastColumn = ws0.Cells(1, Columns.Count).End(xlToLeft).Column Data = ws0.Range(ws0.Cells(2, 2), ws0.Cells(LastRow, LastColumn)).Value Data_T = WorksheetFunction.Transpose(Data) Data_all = ws0.Range(ws0.Cells(1, 1), ws0.Cells(LastRow, LastColumn)).Value N = LastRow - 1 k = LastColumn - 1 D = Data |
次に、共分散を計算しています。行列だけの計算 5 では上手く動かせなかったので、成分毎に計算しました。また、S_inv に共分散の逆行列を格納しています。これはもちろん大事です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
'共分散の計算 ReDim h(k) For i = 1 To k S = 0 For j = 1 To N S = S + Data(j, i) Next j h(i) = S / N Next i For i = 1 To k For j = 1 To N D(j, i) = (Data(j, i) - h(i)) / N Next j Next i D_T = WorksheetFunction.Transpose(D) Sigma = WorksheetFunction.MMult(D_T, D) Sigma_inv = WorksheetFunction.MInverse(Sigma) |
最後にカイ二乗統計量を計算して、95%点を超えるかどうか判定しています。大事です。その後に、dataシートに入っているデータをコピーしてresultシートにも張り付けています。
最後は結果を見やすくするためだけの処理です。6
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
'カイ二乗関連の計算と判定結果の記録 C = WorksheetFunction.MMult(WorksheetFunction.MMult(Data, S_inv), Data_T) ReDim chi(N), test(N) chi_M = WorksheetFunction.ChiSq_Inv(0.05, k) For i = 1 To N chi(i) = C(i, i) If chi(i) < chi_M Then test(i) = "正常" Else test(i) = "異常" End If ws1.Cells(i + 1, 1) = test(i) If ws1.Cells(i + 1, 1) = "異常" Then ws1.Cells(i + 1, 1).Font.Color = RGB(255, 0, 0) End If Next i ws1.Cells(1, 1) = "test" 'resultシートにもデータの写しを作成する For i = 1 To N + 1 For j = 1 To k + 1 ws1.Cells(i, j + 1) = Data_all(i, j) Next j Next i |
マクロの使用方法
excelファイルに、データをコピー＆ペーストして使う事を想定しています。
使い方は以下のようになります。
1.データは以下の写真のように成形して、dataシートに貼り付ける。
2.マクロ7を実行する
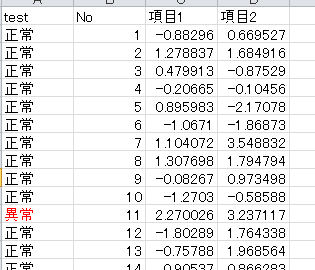
データを正しく成形していれば、result シートに判定結果が出力されます。
この記事が有用だと思ったら、pythonやRで同じことをしてみてください。8
あえてVBAでやる必要は、今の時代全くないです。
まとめ
- ホテリングのT2理論を簡単に解説した
- 問題設定の説明をした
- VBAで実装した
- 使い方を簡単に説明した
- 横方向に項目が並んでいて、セルを上下に移動すると、別のデータになっているイメージです。
- pythonは可読性が高く、numpy が偉大だという事に気付かされました。
- M>1でしか動作確認して無いので、変な事になるかもしれません。
- データの大きさなど
- worksheetfunctionのmmlutで計算するという事です。無頓着に変数を使うと、配列[だったりそうじゃなかったりして動きませんでした。
- pythonのnumpy みたいにvbaを動かすコツがあれば教えて欲しいです。例えば、共分散行列の計算を、成分毎にやらない方法など知りたいです。
- Hotellingという名前で記憶されているはず
- python での実装は、ブログの中にあります。
