説明変数が多数ある場合の回帰分析について解説します。変数が大量にある場合は、行列を使って計算すると簡単に計算出来ます。この手法が単回帰分析の拡張になっている事を見ていきましょう。
単回帰分析の記事はこちら。

重回帰分析とは
説明変数が1つの時の回帰分析はを単回帰分析と呼びました。説明変数が2つ以上あるある場合は重回帰分析と呼びます。モデルは、以下のようになります。
[mathjax] $$ \begin{eqnarray}
y = \beta _0+ \beta_1 x_1 + \cdots +\beta_m x_m
\end{eqnarray} $$
つまり、データを最も精度よく表す\( \beta_0 , \cdots , \beta _m \)を決める問題です。
説明変数1つだけでデータを説明出来ることは殆どありません。単回帰分析の記事で使った体重と身長のデータを使いましょう。 性別毎に体重と身長で散布図を描き、単回帰分析で作った直線をフィットさせてみます。
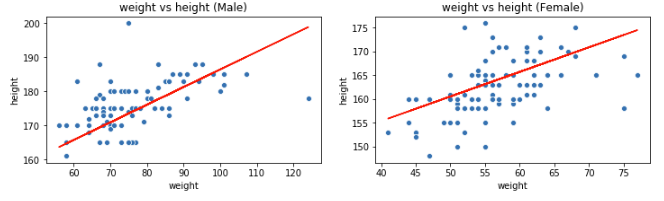
男性と女性とでは身長と体重の範囲に大きな差があります。単回帰分析の記事では、体重だけから身長を予測しましたが、男性か女性かを情報に入れる事で予測の精度が上がりそうです。男性か、女性か分かるようにデータを加工してみましょう。
男性か女性かを識別するための説明変数として sex_F ,sex_M を追加しました。また、性別ごとに直線の傾きが変わって欲しいので体重も性別で区別が着くようにしました。このデータを使って重回帰分析を行ってみましょう。同じように散布図に回帰直線を描いてみます。
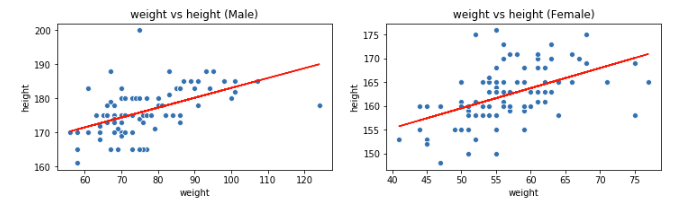
やってみたのは良いものの、変化があるのかどうか良くわかりませんね。単回帰分析では[mathjax] \( R^2\)誤差で精度を評価しました。重回帰分析でも同じように評価できれば、新しく取り入れた説明変数で精度が上がったか確かめられそうです。
単回帰分析の時と同様に、最小二乗法を用いて [mathjax]\( \beta_0 , \cdots , \beta _m \) を決定し[mathjax] \( R^2\) 誤差 と同じ指標を作ってみましょう。
重回帰分析における最小二乗法
以下では、行列やベクトルを使って結果をすっきり見せます。やることは一次の連立方程式を解くだけですが、連立方程式を、手で計算するのは得策ではありません。線形代数の知識があれば連立方程式が完全に解けるかどうかも含めて、簡単に分かります。最小二乗法を行う為に、誤差関数[mathjax]\( e_i \) を導入して、データが以下の式で表せると仮定しましょう。1
[mathjax] $$ \begin{eqnarray}
y_i = \beta _0+ \beta_1 x_{i1} + \cdots +\beta_m x_{im} +e_i
\end{eqnarray} $$
[mathjax]\( x_{ij} \)で, [mathjax]\( j \) 個目の説明変数の、 [mathjax]\( i \)番目のデータを表しました。以下の量を最小にするような [mathjax]\( \beta _0 , \cdots , \beta _m \) を求めましょう。
$$ \begin{eqnarray}
S :=\sum e_i ^2 &=& \sum ( y_i – (\beta _0+ \beta_1 x_{i1} + \cdots +\beta_m x_{im}))^2 \\
&=& \| \vec{y} -X\vec{\beta} \| ^2
\end{eqnarray} $$
各iに対して \( \beta _0 , \cdots , \beta _m \) で偏微分して0と置き、 \( \beta _0 , \cdots , \beta _m \) について解きます。\( \beta \)についての勾配を\( \nabla _{\beta} \)で表すと、以下のように計算出来ます。2
$$ \begin{eqnarray}
\nabla _{\beta} \left( S \right) _{i} &=&
\nabla _{\beta} \left( (\vec{y} -X\vec{\beta} )^{T} ( \vec{y} -X\vec{\beta} ) \right) _i \\
&=& \frac{\partial}{\partial \beta _{i} } \left( (y_k – x_{kj} \beta _{j} )^2 \right) \\
&=& -2 \delta_{ij}x_{kj} ( y_k – x_{kj} \beta _{j})\\
&=&-2\left( X^{T}( \vec{y} -X\vec{\beta} ) \right) _{i}
\end{eqnarray} $$
この計算から、
$$ \begin{eqnarray}
\nabla _{\vec{\beta}} S= -2X^T \vec{y} +2X^{T} X \vec{\beta} =0
\end{eqnarray} $$
となります。この式を解いて
$$ \begin{eqnarray}
\vec{\beta} = \left( X^{T} X \right) ^{-1} X^T \vec{y}
\end{eqnarray} $$
として終わっても良いのですが、もう少し詳しく計算してみます。上の式が解けない場合もあるので、その辺りも詳しく見ましょう。
\( \beta _0 \)に関しては、
$$\begin{eqnarray}
\beta _0 = -\bar{y} + \beta _{i} \bar{x_i}
\end{eqnarray}$$
となるので、これを勾配の式に代入して、\( \beta_1 , \cdots , \beta _m \) についての連立方程式だと思って解きます。綺麗に式をまとめるために以下の量を導入します。3
[mathjax] $$ \begin{eqnarray}
S_{jk}=S_{kj} &=& \sum_{i} (x_{ij} – \bar{x_j})(x_{ik}-\bar{x_k})\\
S_{jy} &=& \sum_{i} (x_{ij}-\bar{x_{j}} ) ( y_i – \bar{y})
\end{eqnarray} $$
4 データと平均値の差を偏差と呼びますが、今定義した [mathjax] \( S_{**}\)は、 [mathjax] \( j , k \) 番目の説明変数の偏差の積となっています。 [mathjax]\( S_{jj} = \sum_{i} (x_{ij} – \bar{x_j}) ^2 \) は、単回帰分析でも出てきていた量です。Sは分散共分散行列と呼ばれます。
\( (j,k) \) 成分を[mathjax]\( S_{jk} \) とする行列を [mathjax]\( \hat{S} \)と置き、 [mathjax]\( \vec{ \hat{\beta} } =(\hat{\beta}_1, \cdots , \hat{\beta}_m ) , \vec{S_y} = (S_{1y}, \cdots , S_{my} ) \) ,
と置きます。すると、連立方程式は以下の形に書けます。
[mathjax] $$ \begin{eqnarray}
\hat{S} \vec{\beta} =\vec{S_y}
\end{eqnarray} $$
もしも[mathjax] \( \hat{S} \)に逆行列が存在すれば、上の連立方程式は解けて、
[mathjax] $$ \begin{eqnarray}
\vec{\beta} = \hat{S} ^{-1} \vec{S_y}
\end{eqnarray} $$
となります。 \( \hat{S} \) に逆行列が存在しない時、\(X \)には多重共線性が存在すると言います。
例えば、特徴量同士に大きな相関がある場合などが、多重共線性が存在する例になります。そんな時は、相関の高いデータを1列残して削除することで、逆行列が存在するようにできます。どうしてもその方法を取りたくない場合は、リッジ回帰を行います。リッジ回帰の解説記事はこちらです。

\( R^2\)誤差を定義して、どんな意味を持っているか確認しましょう。
重回帰分析の場合の[mathjax] \( R^2\)誤差
単回帰分析では、求めた回帰直線がデータの平均値\( \bar{y} \)を説明しているという事を利用して、\( R^2\)誤差を定義していました。同じことは出来るでしょうか?
先ほど求めた [mathjax]\( \beta _0 , \cdots , \beta _m \) でデータを書くと、以下のようになります。
[mathjax]$$ \begin{eqnarray}
y_i &=& \hat{\beta} _0 + \sum_{j} (\hat{\beta}_j x_{ij}+e_{j} )\\
\hat{y} _i &=& \hat{\beta} _0 + \sum_{j} \hat{\beta}_j x_{ij}
\end{eqnarray}$$
上の式で平均値を取ると、
[mathjax]$$ \begin{eqnarray}
\bar{y} = \hat{\beta} _0 + \sum_{j} (\hat{\beta}_j \bar{x}_{j} )
\end{eqnarray}$$
となり、今回の結果もデータの平均値を説明できるものになっています。つまり、以下のバラツキは回帰式で説明できます。
[mathjax]$$ \begin{eqnarray}
S_R = \sum(\hat{y}_i -\bar{y})^2
\end{eqnarray}$$
[mathjax]\( y \) のバラツキ全体は、 [mathjax]\( S_{yy} = \sum (y_i -\bar{y} )^2 \)と書けるので、重回帰分析で説明出来るバラツキは
[mathjax]$$ \begin{eqnarray}
\frac{S_R}{S_{yy}}
\end{eqnarray}$$
となります。 これを、[mathjax] \( R^2 \)誤差として定義できます。計算するとまたしても[mathjax]\( S_{yy}=S_R + \sum(\hat{y}_i -y_i )^2 = S_R +S_e \)が成り立つことが分かり、
[mathjax]$$ \begin{eqnarray}
R^2 =\frac{S_R}{S_{yy}}= 1 – \frac{S_e}{S_{yy}}
\end{eqnarray}$$
となります。ちなみに、身長と体重のデータを加工して重回帰分析を行うと[mathjax] \( R^2\)誤差は0.66 となります。
単回帰分析の時は0.58だったので、僅かに精度が向上している事が分かります。変数が大量にあるとどうなるでしょうか。きっと精度が向上するでしょうが全く意味のない説明変数が増えたらどうなるでしょうか。もちろん精度は上がりませんが、\( R^2\)誤差 は1に近付いてしまいます。そのことについて以下で説明します。
重回帰分析における説明変数の数
[mathjax] \( R^2\)は [mathjax] \( \frac{S_R}{S_{yy}} \) が大きければ、大きな値を取ります。 [mathjax] \( S_R \)は バラツキを含めてデータを説明できるような説明変数があれば大きくなり、 [mathjax] \( R^2\)も大きくなります。 しかし、 [mathjax] \( \frac{S_R}{S_{yy}}\) を大きくする方法はもう一つあります。それは、単純に説明変数を増やすことです。説明変数が減ろうが増えようが[mathjax]\( S_{yy}\) は変化しませんが、 [mathjax]\( S_{R}\)は大きくなっていきます。
よって、正確に精度を計るためには説明変数の数でペナルティをつける必要があります。
[mathjax]$$ \begin{eqnarray}
\tilde{R}^2 &=& 1 – \frac{S_e/\phi _e}{S_{yy}/\phi _T}\\
\phi _T &=&N-1\\
\phi _e &=&N-m-1
\end{eqnarray}$$
\( \phi \)は自由度と呼ばれます。 単純には、データ数-1 の量のことです。データ数と平均値を変化させずにデータを弄ろうと思うと、データ数-1 個のデータを弄れるから自由度=(データ数)-1です。説明変数が大量にあると、それだけで [mathjax] \( R^2\) が大きくなり、精度が上がったかの錯覚に陥るので注意が必要です。説明変数が大量にある場合の事を書きましたが、説明変数が1つだけの時はどうなるのでしょうか。
単回帰分析の再現
[mathjax] \( m=1 \)とすることで、単回帰分析を再現することは出来るでしょうか。[mathjax] \( \beta \)達の決定に関しては 、単回帰分析の場合から連立方程式が多くなっているだけなので、同じ結果が得られる事が分かると思います。
[mathjax] \( R^2\)誤差はどうでしょうか。単回帰分析の場合で大事な所は、データの平均は回帰直線で説明できるとした上で、計算で以下の式を導出した所でした。
[mathjax]$$\begin{eqnarray}
\sum(y_i – \bar{y})^2
&=&
\sum (y_i -\hat{y_i})^2 +\sum \hat{e_i} ^2 \\
&=&
\sum (y_i -\hat{y_i})^2 + \sum (\hat{y_i} – \bar{y})^2
\end{eqnarray}$$
上の式を[mathjax] \( \sum(y_i – \bar{y})^2 \)で割り、移項すると重回帰分析の時の [mathjax] \( R^2\)誤差と同じ形が出てきます。以上から、重回帰分析は、単回帰分析の拡張となっていることが分かりました。
まとめ
・説明変数が2つ以上の回帰問題を重回帰分析と呼ぶ。
・最小二乗法を使うことで、パラメーター [mathjax]\( \beta _0 , \cdots , \beta _m \) を求められる。
・単回帰分析と同様の考え方で \( R^2\)誤差を定義する事が出来る。
・説明変数が多い時や説明変数を変えた時の精度を評価するときは[mathjax]\(\tilde{R}^2\)を使う。
・重回帰分析は、単回帰分析の拡張となっている。
- 以下の記事で、\( e_i \) の意味を解説しています。https://masamunetogetoge.com/bayes-regression
- アインシュタインの縮約を使っています。同じ添え字については和をとります。例えば、\( x_i y_i =\vec{x} \cdot \vec{y} = \sum_{j} x_{j} y_{j} \)などになります。
- \( S= (\vec{x} – \vec{\mu} )(\vec{x}- \vec{\mu} )^{T} \)と置いています。
- \( X^{T} X \vec{\beta} = X^T \vec{y} \) は\(m+1\)次元ベクトルの式ですが、\(S \)を使うと\(m \)次元の式になります。

