のっぴきならぬ事情により、python などで計算を行う事が出来ない人もいるかもしれません。そのような人の為に、エクセルだけで完結するコンテンツを作ります。 1
今回の記事では、混合正規分布によって、データを分類します。混合正規分布のパラメーターの推定には、EMアルゴリズムを使います。
今回の記事は、VBAでEstepまで実装します。
問題設定
データを混合正規分布で近似する目的は複数あります。
- データをクラスタ分けする
- データに含まれるクラスタの比率を推定する
- クラスタ毎の平均と分散を推定する
上記3つが主な目的です。やりようによっては、クラスタの数Kも推定する事が出来ますが、今回の記事では、Kは人間が与える事にします。
この記事の手法を使うのは、以下のような状況です。
- 複数の山を持つデータを取り合えずクラスタ分けしたい
- データが持つそれぞれの山の平均値や分散が知りたい
- 異常検知手法として使い、異常なデータがどんな振る舞いをするか調べたい
混合正規分布
混合正規分布については、以下の記事で詳しく説明しています。
どんな確率モデルを使うのかだけ解説しておきます。
混合正規分布では、データ\( X= \{x_1 , \cdots , x_N \} \)が次のような過程に沿って生成されていると考えます。
- データをクラスタ\(1,\cdots , K \)を割り当てる確率分布\( p( \pi ) \)があり、混合比率\( ( \pi _1 , \cdots , \pi _K ) \)が決まる。
- 各kに対して、パラメータ\( \theta _k = (\mu _k , \Sigma _k )\)が事前分布\( p ( \theta _k ) \)から生成される。2
- データ\(x_n \) に対応するクラスタの割り当て\(s_n \)が比率\( \pi \)から選ばれる。
- \( s_n \)によって選ばれたk が、\( x_n \)のクラスタ番号になる。また、データ\( x_n \)が\( p(x_n |\theta _k ) \)で生成される。
モデルの気持ちは上記の通りですが、実際に使う式とモデルの図を列挙しておきます。
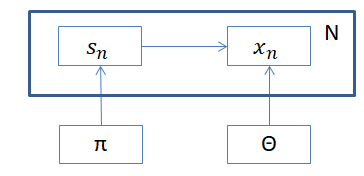
\(x_n \)のクラスタkが決まっている時、正規分布から生成されていると考えるのが、混合正規分布モデルです。3
$$\begin{eqnarray}
p(x_n | \theta _k ) = \mathcal{N} (x_n | \mu _k , \Sigma _k )
\end{eqnarray}$$
クラスタは\(s_n \)によって与えられます。\( \pi \)をパラメータにしたカテゴリー分布を使います。
$$\begin{eqnarray}
p(s_n | \pi ) = { \rm Cat } (s_n |\pi ) =\prod _{i=1} ^{K} \pi _i ^{s_{n, i}}
\end{eqnarray}$$
ただし、\(s_n \)はK次元のベクトルで、一つの成分だけが1で、それ以外の成分が0になっています。また、\(\sum _{i=1}^{K}\pi _i =1 \)です。
\(s_n \)の情報がある時、\(x_n \)を生成する確率分布は以下のようになります。
$$\begin{eqnarray}
p(x_n | s_n , \Theta ) = \prod_{k=1}^{K} p(x_n | \theta _k ) ^{s_{n,k} }
\end{eqnarray}$$
本来は、\( \pi \)やパラメーター\( \Theta \)も確率分布から生成されていると考えますが、今回は簡単の為に、定数として扱い、最尤法で推定されるべきパラメーターと考えます。
データ\(x \)自身が従う確率分布は、今までの仮定を使って以下のように計算されます。
$$\begin{eqnarray}
p(x_n ) &=& \sum _{s_n } p(s_n ) p(x_n | s_n , \Theta ) \\
&=&\sum _{k=1} ^{K} \pi _{k} \mathcal{N}(x_n | \mu _k , \Sigma _k )
\end{eqnarray}$$
ただし、\( \sum _{s_n } \)は、取り得る\(s_n \)すべてについて和を取るという意味です。4
\(p(x_n ) \)達を尤度だと思って、最尤法によりパラメータ\( \mu _k , \Sigma _k , \pi _k \)を決定していきます。
$$\begin{eqnarray}
L= \prod_{n=1}^{N} p(x_n)
\end{eqnarray}$$
その為に、EMアルゴリズムと呼ばれる手法を使います。
EMアルゴリズム
尤度に対して、最尤法を使うと、補助変数\( \gamma (s_{n,k} ) \)を使って以下のように推定値が求められます。
$$\begin{eqnarray}
\mu _k &=& \frac{ \sum_{n} \gamma (s_{nk}) x_n }{N_k} \\
\Sigma _k &=&
\frac{1}{N_k} \sum_n \gamma (s_{nk} ) (x_n -\mu_k ) (x_n – \mu _k ) ^{T} \\
\pi _k &=& \frac{N_k }{N} \\
\gamma(s_{nk}) &=&
\frac{ \pi_k \mathcal{N} \left( x_n| \mu _k , \Sigma _k \right) }{ \sum_j \pi_j \mathcal{N} \left( x_n| \mu _j , \Sigma _j \right) } \\
N_k &=& \sum_n \gamma (s_{nk} )
\end{eqnarray}$$
\( \mu ,\Sigma , \pi \)は一応式の形が分かりますが、\( \gamma (s_{n,k } ) \)達に依存しているので、解けたわけではありません。EMアルゴリズムでは、次のように段階的にパラメーターを求めます。
[E ステップ]
\( \mu _k , \Sigma _k , \pi _k \)を適当に与え、\( \gamma (s_{n,k} ) , N_k \)を計算する。
[Mステップ]
\( \mu _k , \Sigma _k , \pi _k \) を計算する。
Eステップ、Mステップの順に繰り返し計算を行い5 、尤度が収束したら計算を終了するのがEMアルゴリズムです。
VBAで実装する
以上の計算を、VBAで実装します。
dataというシートにデータが有るという前提で、以下の手順で計算させます。諸々の計算は、result シートを使います。6
- データの形を取得する(データの数、次元)
- クラスタ数Kを聞くメッセージボックスを表示する
- 1,2の情報から,\( \mu _k , \Sigma _k , \pi _k \)を適当に与える。
- EMアルゴリズムに沿って計算する
今回は、4.の途中である、Estep の計算までを実装します。7
'Estepまでのコード
Sub GMM()
'変数の定義
Dim LastRow, LastColumn
Dim Data, Data_T
Dim ws0, ws1 As Worksheet
'worksheet の指定
Set ws0 = Worksheets("data")
Set ws1 = Worksheets("result")
'データの情報を取得する
LastRow = ws0.Cells(Rows.Count, 1).End(xlUp).Row
LastColumn = ws0.Cells(1, Columns.Count).End(xlToLeft).Column
Dim N As Integer, M As Integer, k As Integer
N = LastRow - 1
M = LastColumn - 1
ReDim Data(0 To N, 0 To M)
Data = ws0.Range(ws0.Cells(2, 2), ws0.Cells(LastRow, LastColumn)).Value
Data_T = WorksheetFunction.Transpose(Data)
Data_all = ws0.Range(ws0.Cells(1, 1), ws0.Cells(LastRow, LastColumn)).Value
D = Data
'msgboxからKの値を受け取る
k = InputBox(prompt:="クラスタの数を入力してください", Default:=2, Title:="K=?")
'Kが整数か判定する
If Not VarType(k) = 2 Then
k = InputBox(prompt:="整数を入力してください", Default:=2, Title:="K=?")
End If
'パラメーターの初期化
Dim pi()
ReDim pi(1 To k)
For i = 1 To k
pi(i) = 1 / k
Next i
Dim mu()
ReDim mu(1 To M, 1 To k)
For i = 1 To M
For j = 1 To k
mu(i, j) = 1 / N
Next j
Next i
Dim Sigma()
ReDim Sigma(1 To M, 1 To M, 1 To k)
For l = 1 To k
For i = 1 To M
For j = 1 To M
If i = j Then
Sigma(i, j, l) = 1
Else
Sigma(i, j, l) = 0
End If
Next j
Next i
Next l
'result シートに値を書き込む
For i = 1 To k
ws1.Cells(1, i).Value = "mu_" + CStr(i)
ws1.Range(Cells(2, i), Cells(2 + M - 1, i)).Value = get_mu_k(mu, (i))
Next i
For i = 1 To k
ws1.Cells(1, k + M * (i - 1) + 1).Value = "Sigma_" + CStr(i)
ws1.Range(Cells(2, k + M * (i - 1) + 1), Cells(2 + M - 1, k + M * i)).Value = get_Sigma_k(Sigma, (i))
Next i
'パラメーターの初期化終わり
'Estep
Dim G As Double
Dim gamma()
ReDim gamma(1 To N, 1 To k)
For i = 1 To N
Dim x_n()
ReDim x_n(1 To M)
For j = 1 To M
x_n(j) = Data(i, j)
Next j
For l = 1 To k
mu_l = get_mu_k(mu, (l))
Sigma_l = get_Sigma_k(Sigma, (l))
Dim y
ReDim y(1 To M, 1 To 1)
For p = 1 To M
y(p, 1) = x_n(p) - mu_l(p)
Next p
Sigma_inv = WorksheetFunction.MInverse(Sigma_l)
shorder = (-1 / 2) * _
WorksheetFunction.MMult( _
WorksheetFunction.MMult(WorksheetFunction.Transpose(y) _
, Sigma_inv), y)(1)
Mnormal = (2 * WorksheetFunction.pi) ^ (-M / 2) * _
WorksheetFunction.MDeterm(Sigma_l) ^ (-1 / 2) * Exp(shorder)
G = G + pi(l) * Mnormal
Next l
For l = 1 To k
mu_l = get_mu_k(mu, (l))
Sigma_l = get_Sigma_k(Sigma, (l))
Sigma_inv = WorksheetFunction.MInverse(Sigma_l)
shorder = (-1 / 2) *
WorksheetFunction.MMult(WorksheetFunction.MMult(WorksheetFunction.Transpose(y), Sigma_inv), y)(1)
Mnormal = (2 * WorksheetFunction.pi) ^ (-M / 2) * WorksheetFunction.MDeterm(Sigma_l) ^ (-1 / 2) * Exp(shorder)
gamma(i, l) = pi(l) * Mnormal / G
Next l
Next i
'gamma_nk をワークシートに書いておく
For i = 1 To k
ws1.Cells(1, k + M * k + i).Value = "gamma_" + CStr(i)
Dim gamma_k()
ReDim gamma_k(1 To N, 1 To 1)
For j = 1 To N
gamma_k(j, 1) = gamma(j, i)
Next j
ws1.Range(Cells(2, k + M * k + i), _
Cells(2 + N - 1, k + M * k + i)).Value = gamma_k
Next i
Dim N_k()
ReDim N_k(1 To k)
For i = 1 To k
N_k(i) = WorksheetFunction.Sum(ws1.Range(Cells(2, k + M * k + i), _
Cells(2 + N - 1, k + M * k + i)))
Next i
End Sub
'μの一部を抜き出す関数
Function get_mu_k(mu(), k As Long)
M = UBound(mu, 1)
Dim mu_k
ReDim mu_k(1 To M)
For i = 1 To M
mu_k(i) = mu(i, k)
Next i
get_mu_k = mu_k
End Function
'Σの一部を抜き出す関数
Function get_Sigma_k(Sigma(), k As Long)
M = UBound(Sigma, 1)
Dim Sigma_k
ReDim Sigma_k(1 To M, 1 To M)
For i = 1 To M
For j = 1 To M
Sigma_k(i, j) = Sigma(i, j, k)
Next j
Next i
get_Sigma_k = Sigma_k
End Function
'データの一部を抜き出す関数
Function get_x_n(X(), k As Integer)
M = UBound(X, 2)
Dim x_n
ReDim x_n(1 To M)
For i = 1 To M
x_n(i) = X(k, i)
Next i
get_x_n = x_n
End Function配列の値を初期化するのに、成分毎で値を設定したので、凄く見づらいコードになってしまいました。8
大事そうな場所だけ解説します。基本的に、定義通りに計算するだけなのですが、python のように配列を作って、配列の一部を取り出そうとしたりすることが(多分)出来ません。
その為に、平均、分散、元データの一部を取り出す関数を作っています。
'μの一部を抜き出す関数
Function get_mu_k(mu(), k As Long)
M = UBound(mu, 1)
Dim mu_k
ReDim mu_k(1 To M)
For i = 1 To M
mu_k(i) = mu(i, k)
Next i
get_mu_k = mu_k
End Function
'Σの一部を抜き出す関数
Function get_Sigma_k(Sigma(), k As Long)
M = UBound(Sigma, 1)
Dim Sigma_k
ReDim Sigma_k(1 To M, 1 To M)
For i = 1 To M
For j = 1 To M
Sigma_k(i, j) = Sigma(i, j, k)
Next j
Next i
get_Sigma_k = Sigma_k
End Function
'データの一部を抜き出す関数
Function get_x_n(X(), k As Integer)
M = UBound(X, 2)
Dim x_n
ReDim x_n(1 To M)
For i = 1 To M
x_n(i) = X(k, i)
Next i
get_x_n = x_n
End Functionまた、多変量正規分布を得る関数が無いので、自力で計算させています。
For l = 1 To k
'クラスタlの平均
mu_l = get_mu_k(mu, (l))
'クラスタlの分散
Sigma_l = get_Sigma_k(Sigma, (l))
'x_n - mu_k の配列
Dim y
ReDim y(1 To M, 1 To 1)
For p = 1 To M
y(p, 1) = x_n(p) - mu_l(p)
Next p
Sigma_inv = WorksheetFunction.MInverse(Sigma_l)
'正規分布の肩の部分の計算,
'結果に成分が1つの配列が返ってくるので、成分を指定して数同士の計算を出来るようにしている
shorder = (-1 / 2) * _
WorksheetFunction.MMult(WorksheetFunction.MMult(WorksheetFunction.Transpose(y) _
, Sigma_inv), y)(1)
Mnormal = (2 * WorksheetFunction.pi) ^ (-M / 2) * WorksheetFunction.MDeterm(Sigma_l) ^ (-1 / 2) * Exp(shorder)mu_l, Sigma_l はクラスタ毎の正規分布の平均と分散です。エクセルについている行列積の関数や、行列の逆行列を求める関数を駆使して計算させています。
以下のようなデータを与えてマクロを実行できます。
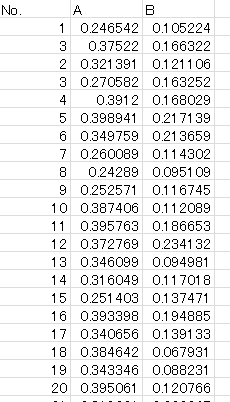
Eステップまでのコードを実行すると、result シートに平均や分散、Γの値が記録されます。
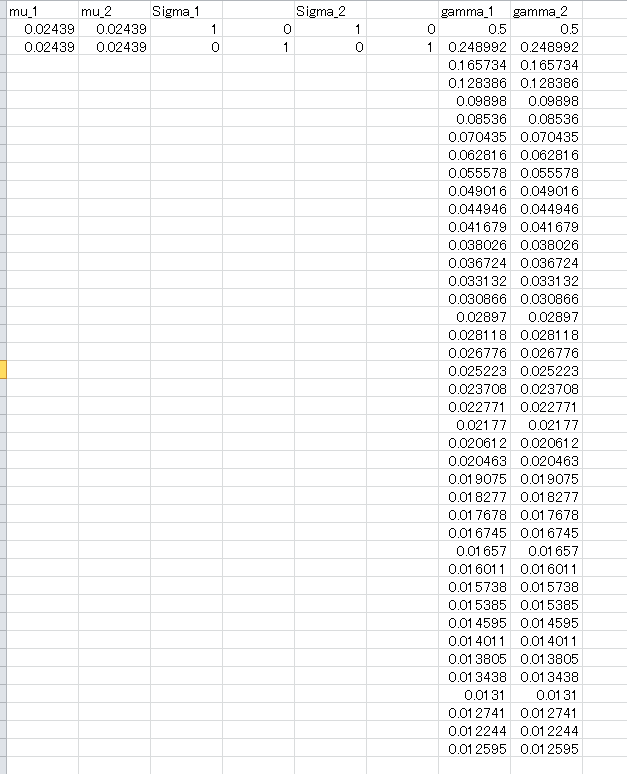
まとめ
- 混合正規分布モデルの説明をした
- EMアルゴリズムの説明をした
- Eステップまでvbaで実装した

