実際にデータを解析するときに、手計算する必要は殆どありませんが、計算出来ないと仕組みが理解出来ません。そこで、偏微分の計算方法と、有用と思われる関数についての例を挙げたいと思います。 定義が気になる人は数学の本を、偏微分の使い方が気になる人は物理の本を読んでください。 高校でも1変数関数の微分を習うと思いますが、それさえ知っていれば計算は出来ます。
偏微分
重回帰分析の記事でも使った偏微分の計算の仕方について解説します。計算は単純で、
指定された変数以外は定数だと思って微分する。
以上です。いくつか例を計算してみます。
[mathjax] $$ \begin{eqnarray}
f(x,y) &=&2x^2+3xy +y^2 \\
\frac{\partial f}{\partial x} &=& 4x +3y \\
\frac{\partial f}{\partial y} &=& 3x + 2y \\
\frac{\partial ^2 f}{\partial y \partial x} &=& 3
\end{eqnarray} $$
偏微分の順序はいつも交換できる訳ではありませんが、気にする必要がある関数は機械学習の中では出てこないと思って良いでしょう。練習の為に、微分の順序が交換出来ない関数を微分してみましょう。
[mathjax] $$ \begin{eqnarray}
f(x,y) = \begin{cases} \frac{x^3 y}{x^2 +y^2}, &(x,y)& \neq 0\\
0 , &(x,y)&=(0,0)
\end{cases} \\
\end{eqnarray} $$
[mathjax] $$ \begin{eqnarray}
\frac{\partial f}{\partial x} &=& \frac{x^2 y( x^2 +3y^2 )}{ (x^2 +y^2)^2}\\
\frac{\partial f}{\partial y} &=& \frac{x^3(x^2 -y^2)}{(x^2 +y^2)^2} \\
\frac{\partial }{\partial y}( \frac{\partial f}{\partial x}) &=&
\frac{x^6 + 3x^2 y^2 (2x^2 – y^2) }{(x^2 +y^2)^3} \\
\frac{\partial }{\partial x}( \frac{\partial f}{\partial y}) &=&
\frac{x^6 +3x^2 y^2 (2x^2 – y^2)}{(x^2 +y^2)^3}
\end{eqnarray} $$
2階の偏微分は、見かけ上は同じ形になっていますが、x=0を固定して [mathjax] \( y\rightarrow 0\)とする場合( [mathjax]\( \frac{\partial }{\partial y}( \frac{\partial f}{\partial x})(0,0) ) \)では0, y=0を固定して [mathjax] \( x \rightarrow 0\) とする場合( [mathjax] \( \frac{\partial }{\partial x}( \frac{\partial f}{\partial y}) (0,0) \) ) では1となります。
一般に、2階偏導関数が存在して、連続なら偏微分の順序は交換してよいです。2階までの偏導関数が存在して、それらすべてが連続、という関数たちを[mathjax] \(C^2\)級と呼びます。普段目にする関数は何回でも微分出来る( [mathjax] \(C^{\infty}\) 級)ので微分の順序1は気にする必要はありません。
連鎖律
偏微分の大事な性質として、連鎖律があります。機械学習ではこれを利用して、説明変数の重要度を測ります。連鎖律とは、以下の性質のことです。
z=f(u,v), u=g(x,y), v=h(x,y) という状況を考える。 この時、以下が成り立つ。
[mathjax] $$ \begin{eqnarray}
\frac{\partial z}{ \partial x} &=& \frac{ \partial z}{ \partial u} \frac{ \partial u}{ \partial x} + \frac{ \partial z}{ \partial v} \frac{ \partial v}{ \partial x} \\
\frac{\partial z}{ \partial y} &=& \frac{ \partial z}{ \partial u} \frac{ \partial u}{ \partial y} + \frac{ \partial z}{ \partial v} \frac{ \partial v}{ \partial y}
\end{eqnarray} $$
これは、1変数関数の合成関数の微分公式の拡張で、fが3変数以上の関数の場合でも成り立ちます。上の式を見ると行列とベクトルでスッキリ書けるような気がします。気になる人はヤコビアンとかヤコビ行列で検索するか、解析学の本か力学の本の座標変換に関する説明を読んでください。
関数の勾配
偏微分を応用して、ある関数の最小値や最大値を調べる事が出来ます。
関数[mathjax]\( f(x_1, \cdots , x_n)\)に対して、勾配[mathjax]\( \nabla f \) を以下で定義します。
[mathjax]$$
\begin{eqnarray}
\nabla (f) = (\frac{\partial f}{\partial x_1}, \cdots , \frac{\partial f}{\partial x_n} )
\end{eqnarray} $$
[mathjax]\( \nabla \) はナブラと読みます。偏導関数を並べただけです。機械学習では、誤差関数の最小値が非常に重要です。1変数関数ならグラフを書けば最大、最小の情報は紙の上に出てきますが、多変数関数では紙にグラフを書くことは普通出来ません。そんな時に、勾配をヒントに最小値を探していくのです。
以下の関数を例に、勾配のイメージを掴みましょう。
[mathjax]$$
\begin{eqnarray}
f(x,y) = x_0 ^2 + x_1 ^2
\end{eqnarray} $$
等高線が円となるような関数です。この勾配は以下になります。
[mathjax]$$
\begin{eqnarray}
\nabla (f) = (2x_0, 2x_1)
\end{eqnarray} $$
この勾配に沿って、関数の等高線を進むと、最小値に到達することが出来ます。
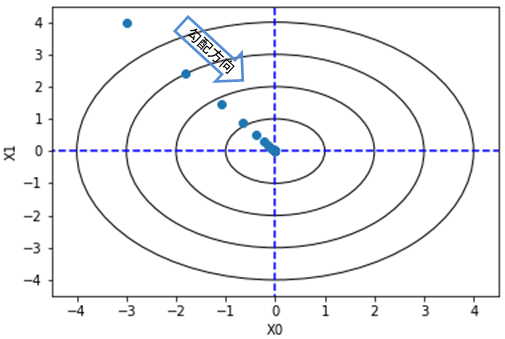
今回は関数が簡単で、最大値は無限大、最小値は0という事が分かっています。大事なのは、関数がどうであれ、勾配を計算しさえすれば、関数の値が小さくなる方向に進んでいけるということです。以下の式を用いて説明変数への入力を更新しています。
[mathjax]$$
\begin{eqnarray}
x^{,} &=& x- \eta \frac{\partial f}{\partial y} \\
y^{,} &=& y- \eta \frac{\partial f}{\partial y}
\end{eqnarray} $$
[mathjax] \( \eta \)は学習率と呼ばれ, 0から1の間で手動で設定する必要のあるパラメーターです。 学習パラメーターは今回は0.1にしています。 上のような式を使って、関数の最小値を探す方法を勾配法と呼びます。
どんな関数でもこの方法で最小値にたどり着けるのでしょうか。単純には出来なさそうです。 関数の形と、スタートする場所によっては極小値にトラップされてしまい、最小値にはたどり着けないかもしれません。1変数関数の3次関数の場合でも簡単に再現出来ます。
この問題を解決する 方法は別の記事で書きたいと思います。
- こういうのが面白いと思う人は数学の本を読みましょう。オススメ本のリンク 貼っておきます。


