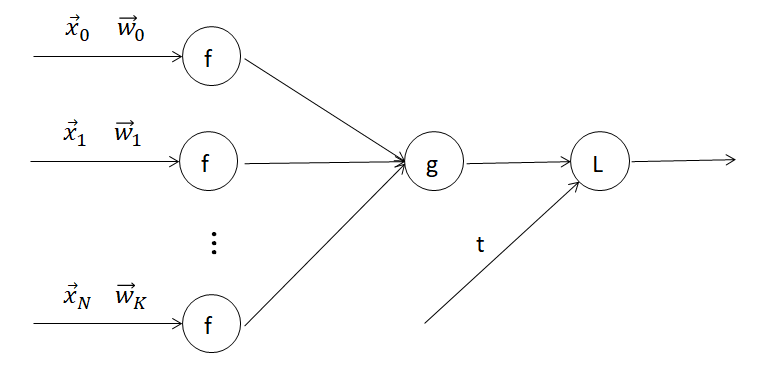
機械学習で必ずと言って良いほど目にする誤差逆伝搬法を解説します。下図のようなモデルを考える時に、パラメーターをどうやって調整したら良いでしょうか?
闇雲に弄ってもしょうがないので、誤差関数を最小にするパラメーターにする。というのが基本の戦略です。誤差関数が微分出来る時は、勾配の流れに沿って誤差を小さくすれば良いのです。これが誤差逆伝搬法の気持ちです。
誤差の伝搬は逆向き?
まず初めに注意しないといけないことは、パラメーターの更新に必要な情報は、パラメーターでの誤差関数の微分であるという事です。誤差関数を最小にするようにパラメーターを調整するのが、分類問題でも回帰問題でも基本の戦略でした。この微分を計算するのに、どんな情報が必要なのでしょうか。
回帰分析の復習はこちら。

ロジスティック回帰(分類問題)の復習はこちら。

誤差関数の値を計算するには、元のデータ、最初に設定したパラメーター、出力関数全てを使う必要がありました。パラメーターの更新には誤差関数の微分を使うので、基本的にパラメーターより入力側の情報は必要ないのです。
当たり前の事なのですが、説明変数から出力を得るには、パラメーターと内積を取って、出力の関数に代入し、必要ならまた内積を取る…と最初から順々に計算していく必要があります。一方で、誤差の情報、つまり誤差関数の勾配は、誤差関数側から、欲しいパラメーターの場所まで最後から逆順に計算するのです。
誤差逆伝搬法
式が煩雑になるだけであまり意味はないのですが、上の説明を数式に起こしてみましょう。第一のパラメータを[mathjax]\( \alpha _0 ,\cdots ,\alpha _n \). 第二のパラメーターを [mathjax]\( \beta _0, \cdots , \beta _n \) で表します。活性化関数は 順に[mathjax]\( f, g \).として、誤差関数は [mathjax]\( E \)と置きます。以下の図のようなモデルをイメージしてください。矢印では内積や積を取ります。
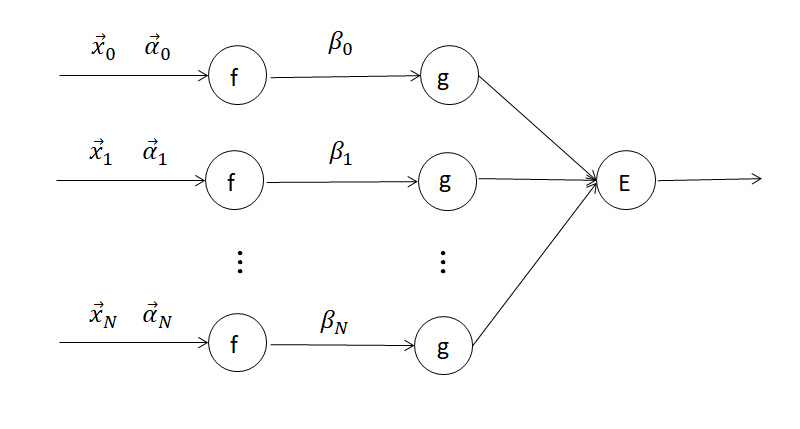
誤差を得るには、以下のように計算する必要があります。
[mathjax]$$ \begin{eqnarray}
E =E(\vec{\alpha}, \beta) = E\big( g(\sum \beta _i f( \vec{x _i} \cdot \vec{\alpha _i} ) ) \big)
\end{eqnarray} $$
[mathjax]\( \beta _j \) の更新の為に、勾配を求めましょう。計算の見通しを良くするために、[mathjax] \( y_i = \vec{x_i} \cdot \vec{ \alpha _i} , z =\sum \beta _i f(y_i) , w= g(z) \) と置きます。
[mathjax]$$ \begin{eqnarray}
\frac{\partial E}{\partial \beta _j} &=&
\frac{\partial z}{\partial \beta _j} \frac{\partial w}{\partial z} \frac{\partial E}{\partial w}
& =& y_j \frac{\partial w}{\partial z} \frac{\partial E}{\partial w}
\end{eqnarray} $$
[mathjax] \( \frac{\partial w}{\partial z} = g’ (z) \)ですが、どうでもよいです。大事なのは、(当たり前なのですが) [mathjax] \( \beta \) の更新には、 [mathjax] \( \beta \) より前の微分は関係ないという事です。
逆に、出力に近いパラメーターが更新されると入力側のパラメーターは影響を受けます。誤差関数は、入力を弄ると出力が変化するのに対して、パラメーターは出力側を弄ると入力側が影響を受けるというある意味逆の現象が起きます。勾配法を用いて、誤差関数を小さくするようにパラメーター一つ一つを更新する手法を逆誤差伝搬法1と言います。
パラメーターの更新は基本的にアルゴリズムに沿って行われます。その最中に’変な事’が起きても普通は処理が止まりません。代表的な’変な事’は勾配消失問題と呼ばれる問題です。パラメーターを更新するための勾配がある時点で0になり、更新されなくなる問題です。別の記事で具体例で説明したいと思います。
こちらの記事で説明しています。
https://masamunetogetoge.com/gradient-vanish
まとめ
・モデルのパラメーター更新をする時に、誤差関数の微分を使おうというのが誤差逆伝搬法の気持ち。
・微分を計算するには、出力側から、パラメータ側までの情報だけで良くて、出力を得るのとは情報の伝わり方が逆。
・原理的に、誤差逆伝搬法ではモデルの入力側のパラメーターは更新されにくい。

