単回帰分析の係数の導出方法とR^2誤差の解説

単回帰分析とは
回帰直線の導出
$ R^2 $誤差
まとめ

単回帰分析とは

単回帰分析について説明します。予測したい量を$y $, 説明に使う変数を$x$とします。¹
単回帰分析とは、$x, y$の間に以下の関係を仮定するモデルの事です。
$$\begin{eqnarray}
y=ax+b
\end{eqnarray}$$
ある意味で、$y$が$x$を最も説明するように、$a,b$を決めるのが目標になります。適当なデータに対して単回帰を適用して、雰囲気を掴みましょう。
身長と体重に関するデータ(RのDavis データ)を使います。
データは性別、身長、体重の3列からなり181個のデータがあります。

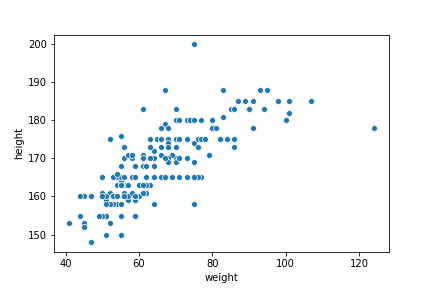
性別は無視して、身長と体重の散布図を見てみましょう。

変な値はありますが、直線でフィット出来そうです。 $y$を身長、$x$を体重として、単回帰分析を行い、グラフに予測された直線を描いてみます。

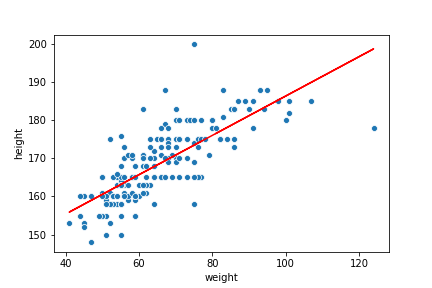
身長と体重の大体の関係はつかめていると思います。この直線の導出の方法と、この直線がどの程度データを説明出来ているかの指標を解説します。

回帰直線の導出

単回帰分析は、$y$と$x$の間に以下の関係を仮定するモデルでした。²
$$\begin{eqnarray}
y=ax+b
\end{eqnarray}$$

基本的に、データはバラツキを持っているので上記のような完ぺきな線形な関係を仮定する事は得策ではありません。そこで、誤差関数$ e_i $たちを導入して、各データ間に次のような関係があると仮定します。
$$ \begin{eqnarray}
y_i =ax_i +b +e_i
\end{eqnarray} $$
誤差関数たちを最小化するような$a,b$ を求めます。このままでは数学的に扱いづらいので、二乗和を取り$S$とおきます。
$$ \begin{eqnarray}
S= \sum e_i^2=\sum ( y_i- (ax_i+b))^2
\end{eqnarray} $$
ただし、和は、全データについて取ります。

$S $ を $a,b $の関数と思って極小値を与える $a,b $ を求めます。具体的には、 $a,b $ での偏微分の値が0になる値を求めます。
$$ \begin{eqnarray}
\frac{\partial S}{\partial a} &=& -2 \sum x_i ( y_i – (ax_i+b) ) =0 \\
\frac{\partial S}{\partial b} &=&- 2 \sum ( y_i – (ax_i+b) ) =0
\end{eqnarray} $$
上式を $a,b $ について解き、その値を $\hat{a}, \hat{b} $ と置くことで、係数が求まります。
ここで、aでの偏微分の式は$ \sum x_i e_i =0 $を意味することに注意しましょう。残差ベクトル$\vec{e} = \{e_i \} $たちは、データ$\vec{x} = \{x_i \} $と直交するという事です。また、$e_i $達の平均が0 という事もあり、各$e_i $の自由度は(データ数) – 2です。
$a, b $の推定値は以下のようになります。
$$ \begin{eqnarray}
\hat{a}&=& \frac{\sum(x_i -\bar{x})(y_i -\bar{y})}{\sum (x_i-\bar{x})^2} \\
\hat{b} &=& \bar{y} -\hat{a}\bar{x}
\end{eqnarray} $$
ただし、データの平均値を文字の上にバーをつけて表しました。
$$ \begin{eqnarray}
\bar{x}&=& \frac{ \sum x_i} {N} \\
\bar{y}&=& \frac{ \sum y_i} {N}
\end{eqnarray} $$
という事です。推定値 $ \hat{a}, \hat{b} $を用いて、求めるべき直線は

[mathjax]$$
\begin{eqnarray}
y= \hat{a}x + \hat{b}
\end{eqnarray} $$

となります。この一連の流れを最小二乗法と言い、求めた直線を回帰直線と呼びます。
余談ですが、[mathjax]$y_i =ax_i +b +e_i $ で両辺の平均値を取ると
$$\begin{eqnarray}
\bar{y} =a\bar{x}+b
\end{eqnarray}$$
となります。このことから、求めた回帰直線は $x_i, y_i $の平均値を説明する直線と考えることが出来ます。初めにDavisデータに対して行った回帰分析も、上記の流れで直線の式が導出されています。
次に、回帰直線がどの程度精度よくデータを再現しているか確かめる尺度を解説します。

$ R^2 $誤差

$ R^2 $誤差と呼ばれる量を定義し、それが回帰直線がどのくらいデータを説明しているかの指標になることを説明します。
理想的にはデータが[mathjax]$y=ax+b$の関係に従っていれば良いのですが、どんなデータも不確実なバラツキをもっています。³ 説明したい変数のバラツキ全体は以下の式で定義されます。
$$\begin{eqnarray}
\sum (y_i – \bar{y} )^2
\end{eqnarray}$$
このバラツキを回帰直線が説明してくれていれば、精度の良い式と言えそうです。回帰直線が説明出来るバラツキは
$$\begin{eqnarray}
S_R = \hat{e_i}^2= \sum (\hat{y_i} – \bar{y})^2
\end{eqnarray}$$
であり、説明出来ないバラツキは
$$\begin{eqnarray}
S_E=\sum (y_i-\hat{y})^2 \
\end{eqnarray}$$
です。そして、計算してみると以下の式が成り立つことが分かります。
[mathjax]$$\begin{eqnarray}
\sum(y_i – \bar{y})^2 = \sum (y_i -\hat{y_i})^2 +\sum \hat{e_i} ^2
\end{eqnarray}$$

$R^2$ 誤差とは、データ全体のバラツキのうち、回帰直線が説明できるバラツキの割合のことです。式で表すと、以下のようになります。
[mathjax]$$\begin{eqnarray}
R^2 := \frac{\sum \hat{e_i} ^2}{ \sum(y_i – \bar{y})^2 }=1-\frac{ \sum (\hat{y_i} – \bar{y})^2 }{ \sum(y_i – \bar{y})^2 }
\end{eqnarray}$$
定義から、$R^2$は0から1の間の値を取り、1に近ければ近い程求めた回帰直線は精度よくデータを表しているという事が出来ます。
明確な決まりはありませんが、$ R^2$誤差は0.6以上で及第点、0.8 以上だと精度良くデータを表していると言われます。ちなみに、一番初めに書いた直線の $ R^2$ は0.58です。精度が良いとは言えない結果です。
精度を上げる方法は2つあります。一つは変なデータを取り除くこと。もう一つは説明するのに使う変数を増やすという事です。
元のデータには性別の情報がありましたが、それも説明変数に加えることで精度を良くすることが出来るかもしれません。次回は、説明変数が2つ以上の場合の回帰直線の求め方を解説します。