カイ二乗分布、t分布の解説記事を書いたので、次はF分布です。
カイ二乗分布や、t分布は一つの正規分布から作る事が出来ますが、F分布は一つの正規分布から作っても意味のあるものは出来ません。
その辺りの話も含めて、詳しく解説します。
参考文献が一応あります。東大出版会の例の本よりはお勧めです。
カイ二乗分布とt分布
F分布を定義するのに、カイ二乗分布が必要です。
詳しい解説は記事があるので読んでみてください。

ついでにt分布も知っているとF分布に親しみやすくなります。

必要な結果だけ書いておきます。
カイ二乗分布は、ガンマ分布の特別な場合です。
$$\begin{eqnarray}
\chi _{n}^2 &=& {\rm Gam}(n/2 , 2 ) \\
{ \rm Gam } (x| \alpha , \beta ) &=& \frac{1}{\Gamma (\alpha )} \frac{1}{\beta} \left( \frac{x}{\beta} \right)^{\alpha -1 } e^{-x/ \beta }
\end{eqnarray}$$
また、標準正規分布に従う独立な確率変数からも得られます。
$$\begin{eqnarray}
Z_1 , \cdots , Z_n &\sim & \mathcal{N} (0,1 ) \\
Z^2&\sim& \chi _{1} ^2 \\
Z_1 ^2 + \cdots + Z_n ^2 &\sim &\chi _{n-1} ^2
\end{eqnarray}$$
正規分布は、標準正規分布に従うように変数変換できたことを思い出すと、正規分布があれば、カイ二乗分布が出て来ます。
$$\begin{eqnarray}
X_1 , \cdots , X_n &\sim & \mathcal{N} (\mu,\sigma ^2 ) \\
Z=(X-\mu)/\sigma &\sim& \mathcal{N} (0,1 ) \\
Z’ =( \sqrt{n} \bar{X} -\mu ) /\sigma &\sim& \mathcal{N} (0,1 )
\end{eqnarray}$$
また、カイ二乗分布を作るには標準正規分布が必要ですが、現実のデータは、正規分布っぽくなっていても、平均=0,分散=1となる事はほぼほぼありません。
標準正規分布を作るために、正確な平均と分散が必要ですが、現実のデータでは推定値を使うしかありません。分散を不偏分散で代用して標準正規分布を作ると、t分布が出て来ます。
$$\begin{eqnarray}
X_1 , \cdots , X_n &\sim & \mathcal{N} (\mu,\sigma ^2 ) \\
V^2 &=& \sum (X_i – \bar{X} )^2 \\
U&=&(n-1)\frac{V^2}{\sigma} \sim \chi _{n-1} ^2 \\
Z&=& \frac{ \sqrt{n} \bar{X} -\mu }{\sigma} \sim \mathcal{N}(0,1) \\
T &=& ( \sqrt{n} \bar{X} -\mu ) /V \\
&=& Z / \sqrt{ U(n-1) } \sim t_{n-1}
\end{eqnarray}$$
F分布とは
F分布は、二つの正規分布の分散の差を比べる為に使います。
単純に2つのデータを比べるという意味でも使いますが、特に大事なのは、回帰分析や分散分析で得られた回帰係数に意味があるか判断することです。
回帰分析や分散分析の記事はこちらをどうぞ。


使い方を話したところで、F分布の定義をします。
[F分布]
S,T を独立な、自由度m,n のカイ二乗分布に従う確率変数とする。
$$\begin{eqnarray}
S &\sim &\chi _{m} ^2 \\
T &\sim &\chi _{n} ^2
\end{eqnarray}$$
このとき、次の確率変数が従う分布を自由度m,n のF分布と呼び、\( F_{m,n} \)で表す。
$$\begin{eqnarray}
\frac{S/m}{T/n} \sim F_{m,n}
\end{eqnarray}$$
確率分布の表式を求めましょう。t分布の時と同様に、力づくで求まります。
\(S,T \)は独立なので、同時確率分布は以下のようになります。
$$\begin{eqnarray}
f(s,t) =\frac{1}{\Gamma (m/2 ) 2^{m/2} } s^{m/2 -1} e^{-s/2} \frac{1}{\Gamma (n/2 ) 2^{n/2} } s^{n/2 -1} e^{-t/2}
\end{eqnarray}$$
\(Z=S/T , W=T\)と置くことで変数変換します。1
初めに、ヤコビアンを求めましょう。\( S=WZ, T=W \)から、
$$\begin{eqnarray}
dt ds &=&\det
\left( \begin{array}{cc}
\frac{\partial s}{\partial z} & \frac{\partial s}{\partial w} \\
\frac{\partial t}{\partial z}& \frac{\partial t}{\partial w} \\
\end{array} \right)
dz dw \\
&=&
\det
\left( \begin{array}{cc}
w& z)\\
0 & 1\\
\end{array} \right)
dz dw \\
&=& w dz dw
\end{eqnarray}$$
となります。これを用いて、\(f(s,t) \)を書き換えると、
$$\begin{eqnarray}
f(s,t) =\frac{1}{\Gamma (m/2 ) \Gamma (n/2) 2^{(m+n)/2} } z^{m/2 -1} w^{(m+n)/2 -1 } e^{-(1+z)w/2}
\end{eqnarray}$$
これを\(w \)で積分して、\(f(z) \)を求めます。
$$\begin{eqnarray}
I(z) = \int_{0}^{\infty} w^{(m+n)/2 -1 } e^{-(1+z)w/2} dw
\end{eqnarray}$$
何となくガンマ関数に似ています。
$$\begin{eqnarray}
\Gamma (t) = \int_{0}^{\infty}y^{-t}e^{-y} dy
\end{eqnarray}$$
変数変換\(x= (1+z)w/2 \)して計算を進めます。
$$\begin{eqnarray}
I(z) &=& \left( \frac{2}{1+z} \right) ^{(m+n)/2} \int_{0}^{\infty} x^{(m+n)/2 -1 } e^{-x} dx \\
&=& \left( \frac{2}{1+z} \right) ^{ (m+n)/2} \Gamma ((m+n)/2 )
\end{eqnarray}$$
これを用いて、
$$\begin{eqnarray}
f(z) =\frac{\Gamma ((m+n)/2 )}{\Gamma (m/2 ) \Gamma (n/2)} \frac{z^{m/2 -1 }}{(1+z)^{(m+n)/2}}
\end{eqnarray}$$
最後に、\(Y=(n/m)Z \)と置けば、\(\frac{dz}{dy} =m/n \)なので、
$$\begin{eqnarray}
F_{m,n} =f(y) =\frac{\Gamma ((m+n)/2 )}{\Gamma (m/2 )\Gamma (n/2)} \frac{(m/n)^{m/2} y^{m/2 -1 }}{(1+(m/n)y )^{(m+n)/2}}
\end{eqnarray}$$
もう一度F分布の定義を書いておきます。
[F分布]
S,T を独立な、自由度m,n のカイ二乗分布に従う確率変数とする。
$$\begin{eqnarray}
S &\sim &\chi _{m} ^2 \\
T &\sim &\chi _{n} ^2
\end{eqnarray}$$
このとき、次の確率変数が従う分布を自由度m,n のF分布と呼び、\( F_{m,n} \)で表す。
$$\begin{eqnarray}
\frac{S/m}{T/n} \sim F_{m,n}
\end{eqnarray}$$
\(F_{m,n} \)の表式は以下のようになる。
$$\begin{eqnarray}
F_{m,n} =f(y) =\frac{\Gamma ((m+n)/2 )}{\Gamma (m/2 )\Gamma (n/2)} \frac{(m/n)^{m/2} y^{m/2 -1 }}{(1+(m/n)y )^{(m+n)/2}}
\end{eqnarray}$$
自由度を適当に変えてF分布のグラフを描いてみます。
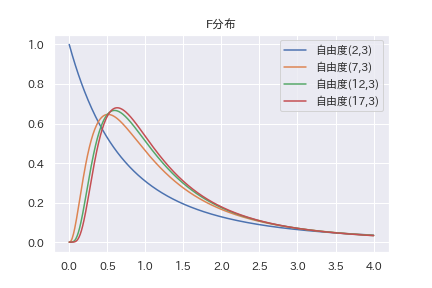
F分布のグラフ 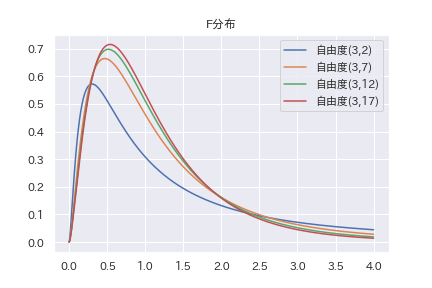
自由度を反転したF分布
\(F_{m,n} \)と\(F_{n,m} \)には一応関係があります。定義から直ちに以下の事が言えます。
\(X \sim F_{m,n} \)ならば、 \( 1/X \sim F_{n,m} \)
F分布とt分布
t分布とF分布には関係があります。t分布が標準正規分布に従う確率変数\(Z \)と、自由度mのカイ二乗分布に従う確率変数\(U \)から作られたこと、\(Z^2 \sim \chi _1 ^2 \)となる事を思い出すと、
$$\begin{eqnarray}
T^2 = Z^2 / (U/m) \sim \chi _1 ^2 /\chi _m ^2 =F_{1,m}
\end{eqnarray}$$
が成り立ちます。この意味で、t統計量とF統計量は同じものと言う人もいます。
また、\( t_m = F_{1,m } \)という意味で、F分布はt分布の一般化になっています。
F分布の使い道
F分布は、2つの正規分布の分散を比べるのによく使われます。(等分散性の検定)
詳しい使い方は回帰分析や、分散分析の記事で解説しているので、問題設定と使い方だけ書いておきます。
[F検定で扱う問題]
\(X_1 , \cdots , X_m \sim \mathcal{N} (\mu _1,\sigma _1 ^2 ), Y_1 , \cdots ,Y_n \sim \mathcal{N} (\mu _2 , \sigma _2 ^2 ) \)がある時、\( \sigma _1 = \sigma _2 \)か?
それぞれの分散の推定値は以下の通りです。
$$\begin{eqnarray}
\hat{\sigma _1 }^2 &=& \sum \frac{( X_i – \bar{X} )^2}{m-1} \\
\hat{\sigma _2 }^2 &=& \sum \frac{( Y_i – \bar{Y} )^2}{n-1}
\end{eqnarray}$$
仮に、\( \sigma _1 = \sigma _2 =\sigma \)だとすると、
$$\begin{eqnarray}
\hat{\sigma _1 } ^2 / \hat{\sigma _2 }^2 = \frac{ \hat{\sigma _1 } ^2 / \sigma ^2}{ \hat{\sigma _2 }^2 / \sigma ^2} \sim \frac{ \chi _{m-1} ^2 /(m-1) }{\chi _{n-1} ^2 /(n-1) } \sim F_{m-1 , n-1}
\end{eqnarray}$$
となり、不偏分散の比がF分布に従います。2この時、有意水準\( \alpha \)を決めて、仮説検定を実行することで、\( \sigma _1 = \sigma _2 \)かを検定する事が出来ます。
F値の出し方的に、\( \sigma _1 \neq \sigma _2 \)と結論付ければ、自動的に\( \sigma _1 > \sigma _2 \)となります。3
おまけ[F分布とベータ分布]
F分布は、少し変数変換すると、ベータ分布として表す事が出来ます。この事を使って、平均や分散がそれなりに簡単に求まります。
S,T を独立な、自由度m,n のカイ二乗分布に従う確率変数とする。
$$\begin{eqnarray}
S &\sim &\chi _{m} ^2 \\
T &\sim &\chi _{n} ^2
\end{eqnarray}$$
\( Z=S/T , W=T \)とし、\(W=S/(S+T) = Z/(1+Z) \)と置くと、4 \(W \)はベータ分布\( {\rm Beta } (m/2 , n/2 ) \)に従う。
$$\begin{eqnarray}
W & \sim &{\rm Beta } (m/2 , n/2 ) \\
{\rm Beta }(x| m , n ) &=& \frac{1}{B(m,n)} x^{m-1} (1-x)^{n-1} \\
B(m,n) &=& \frac{\Gamma (m ) \Gamma (n)}{\Gamma (m+n) }
\end{eqnarray}$$
計算すれば分かるので、少し頑張ってみましょう。
$$\begin{eqnarray}
f(z) =\frac{\Gamma ((m+n)/2 )}{\Gamma (m/2 ) \Gamma (n/2)} \frac{z^{m/2 -1 }}{(1+z)^{(m+n)/2}}
\end{eqnarray}$$
を思い出すと、係数部分のベータ関数は既にあります。
\(z=w/(1-w) , dz/dw = 1/(1-w)^2 \)を代入しましょう。
$$\begin{eqnarray}
f(w) &=&\frac{\Gamma ((m+n)/2 )}{\Gamma (m/2 ) \Gamma (n/2)} w^{m/2 -1 } (1-w)^{n/2 -1} =
{\rm Beta }(w| m/2 , n/2 )
\end{eqnarray}$$
これでベータ分布が出てくることが分かりました。
次に \( y= (n/m)z \)なので,
$$\begin{eqnarray}
y&=& \frac{ (n/m)w}{1-w} \\
f(y)dy &=& (n/m)f(w) dw
\end{eqnarray}$$
となります。この関係式を使うと、F分布の期待値たち(モーメント)は、以下のように計算出来ます。
$$\begin{eqnarray}
E[Y^l] = (n/m)^l \frac{ {\rm Beta }(m/2 +l , n/2-l )}{{\rm Beta }(m/2 , n/2 )}
\end{eqnarray}$$
もちろん、ベータ関数は、n,mの組み合わせ次第では発散しますが、今はあまり気にしないことにします。
ベータ関数達の計算が必要になりますが、計算はガンマ関数に関する公式を使います。
$$\begin{eqnarray}
\Gamma (a+1) = a \Gamma (a)
\end{eqnarray}$$
この公式を使うと、例えば
$$\begin{eqnarray}
\Gamma (m/2+1) / \Gamma(m/2) &=&m/2 \\
\Gamma (n/2 -1) / \Gamma(n/2) &=& \frac{1}{n/2 -1}
\end{eqnarray}$$
などと計算が出来ます。
これを踏まえて、F分布の平均値は、
$$\begin{eqnarray}
E[Y] &=& (n/m) \frac{ {\rm Beta }(w| m/2 +1 , n/2 -1 )}{{\rm Beta }(w| m/2 , n/2 )} \\
&=& (n/m ) \frac{m/2}{n/2 -1} \\
&=& \frac{n}{n-2}
\end{eqnarray}$$
同様にして、
$$\begin{eqnarray}
E[Y^2] &=& (n/m) \frac{ {\rm Beta }(w| m/2 +2 , n/2 -2 )}{{\rm Beta }(w| m/2 , n/2 )} \\
&=& (n/m)^2 \frac{(m+2)m}{(n-2)(n-4)}
\end{eqnarray}$$
が求まるので、分散は
$$\begin{eqnarray}
Var[Y]&=& E[Y^2] -(E[Y])^2
&=&\frac{2m^2 (m+n-2 )}{m (n-2)^2 (n-4)}
\end{eqnarray}$$
と求まります。
まとめ
- カイ二乗分布やt分布の定義を復習した
- F分布の定義をした
- F分布の表式を求めた
- F分布の使い方を解説した
- F分布の平均値や分散を求めた

