機械学習でも、統計学でも、何かパラメーターを決める為に、最小二乗法1 を使う事があります。最小二乗法の導入は、\( | \hat{y} -y | \)だと数学的に扱いにくいから二乗しましょうとかですが、実は最小二乗法で求められた推定量は統計的に良い性質を持っています。
その良い性質を理解して、大手を振って最小二乗法を使っていこうという記事です。
記事で使っているソースコードはgithub に置いてあります。
https://github.com/msamunetogetoge
参考書です。
https://amzn.to/2Wbpkaz
推定量の種類と例
データの統計量(母集団の平均や分散など)を推定する時、それらを評価するために名前を付けておくと便利です。2
最小二乗法の素晴らしさを語るために、不偏推定量を定義します。
[不偏推定量]
データがある確率分布からサンプルされていると仮定しましょう。
$$\begin{eqnarray}
X_1 , \cdots , X_n & \sim & p(x |\theta )
\end{eqnarray}$$
データ\(X_i \)たちから、\( \theta \)を推定して\( \hat{\theta} (X) \)を得たとします。
期待値が\( \theta \)に一致する時、\( \hat{\theta} (X) \) を不偏推定量と呼びます。
$$\begin{eqnarray}
E[\hat{\theta} (X) ] =\theta
\end{eqnarray}$$
不偏推定量は、平均的に見れば、統計量を正確に推定できている量というイメージです。
不偏性を判断するための量として、バイアスがあります。
$$\begin{eqnarray}
Bias(\theta ) = E[\hat{\theta}] -\theta
\end{eqnarray}$$
不偏推定量である事と、バイアスが0である事は同値です。
不偏推定量の例を見る為に、例えば、データが正規分布からサンプルされている時を考えましょう。平均値の不偏推定量を考えます。3
$$\begin{eqnarray}
X_1 , \cdots , X_n & \sim & \mathcal{N}(\mu , \sigma ^2)
\end{eqnarray}$$
この時、平均\( \mu \)の不偏推定量の例として、\(X_1 , \bar{X} =\sum X_i /n \),などがあります。
不偏性だけが欲しいなら、データ一つだけでも不偏推定量になります。
\(X_1 \)と\( \bar{X} \)の違いは何でしょう?
以下で詳しく見てみます。
推定量の評価
推定量\( \hat{\theta} \)を考えるにあたって、不偏性だけを課すと、あまり信用にならなさそうな値も推定量として使えてしまう事が分かりました。平均的に見た時に良いだけではなくて、値としてのバラツキが小さいほうが嬉しいと思うのが人間です。
そこで、推定量の分散を以下で定義しましょう。4
$$\begin{eqnarray}
Var (\theta ) = E\left[ (\hat{\theta} -E[\hat{\theta }] )^2 \right]
\end{eqnarray}$$
不偏でかつ、分散が小さい推定量が良い推定量だと思いましょう。この基準で\( X_1 , \bar{X} \)を比べてみます。5
$$\begin{eqnarray}
Var (X_1 ) &=& E\left[ (X_1 -E[X_1] )^2 \right] \\
&=& E[( X_1 ^2 -2X_1\mu + \mu ^2 ]\\
&=& E[X_1 ^2] – \mu ^2 \\
&=& \sigma ^2
\end{eqnarray}$$
次に、\( \bar{X} \)の方を計算します。\( \bar{X} \sim \mathcal{N} (\nu, \sigma ^2 /n ) \)に従う事に注意すると、
$$\begin{eqnarray}
Var (\bar{X} ) = \sigma ^2 /n
\end{eqnarray}$$
となります。つまり、
$$\begin{eqnarray}
Var (\bar{X} ) < Var (X_1 )
\end{eqnarray}$$
であることが分かります。今回の状況だと、線形な不偏推定量のうち、分散を最小にするのは\( \bar{X} \)であることが示せます。6
一般に、線形な推定量のうち、分散を最小にする推定量の事を最良線形不偏推定量(best linear unbiased estimator; BLUE)と呼びます。7
言葉の準備はこれくらいにして、最小二乗法の素晴らしさを語っていきたいと思います。
最小二乗法
最小二乗法とは、パラメーターなどを推定する時に、\( L= E[( \hat{\theta } -\theta)^2 ]\)を最小にする推定量を求める手法の事です。\(L \)を少し書き換えましょう。
$$\begin{eqnarray}
L&=& E[ ( \hat{\theta} -E[\hat{\theta}] + E[\hat{\theta}] -\theta )^2 ]\\
&=& E[ ( \hat{\theta} -E[\hat{\theta}] )^2] + E[ ( E[\hat{\theta}] -\theta )^2 ] \\
&=& Var(\theta ) + Bias(\theta)^2
\end{eqnarray}$$
Lは、バイアスと分散が1:1の割合で重みづけされた関数だったのです。
Lを最小化するというのは、バイアスと分散どちらも同じくらい最小化しなさい、という誤差だったわけです。二乗誤差を使う時は、不偏推定量を考える限りでは、推定量の分散に一致します。
つまり、\( E[\hat{\theta } ] =\theta \)の時、
$$\begin{eqnarray}
L&=& E[ ( \hat{\theta} -E[\hat{\theta}] + E[\hat{\theta}] -\theta )^2 ]\\
&=& Var(\theta )
\end{eqnarray}$$
です。
この事から、二乗誤差を考えている時、線形な不偏推定量で誤差を最小に出来ると、BLIUEが出て来ます。8
最小二乗法に初めて出会うであろう回帰分析で確かめてみましょう。
回帰分析の回帰係数はBLUE!!!
回帰分析の詳しい計算などは、回帰分析の記事を読んでもらう事にして、回帰分析で求まる回帰係数がBLUEになっている事を確かめたいと思います。
データから出来る行列を\(X \), 予測したいデータを\( y \), 誤差関数を\( u \sim \mathcal{N}(0,\sigma ^2 I )\)とします。9
回帰分析は、
$$\begin{eqnarray}
y=X\beta + u
\end{eqnarray}$$
という関係を仮定して、\(y \)から\( \beta \)を推定する問題です。
\( \hat{y} = X\hat{\beta} \)として、最小二乗法を行います。つまり、
$$\begin{eqnarray}
min_{\beta } E[(y-\hat{y} )^2]
\end{eqnarray}$$
という事です。\( \hat{\beta } \)がBLUEになる事を示していきます。ちなみに、求まる回帰係数は、
$$\begin{eqnarray}
\hat{\beta} = (X^T X )^{-1} X^T y
\end{eqnarray}$$
でした。
\( \beta \) の線形推定量は\(y \)と、行列Cを用いて
$$\begin{eqnarray}
\hat{\beta} = Cy
\end{eqnarray}$$
と書けます。また、不偏推定量であるには、
$$\begin{eqnarray}
E[ Cy] &=& E[CX\beta ] +E[Cu]\\
&=&CX\beta =\beta
\end{eqnarray}$$
より、\(CX=I \)が必要です。最小二乗法で求めた\( \hat{\beta} \)はこれを満たしています。
次に、分散を計算します。
$$\begin{eqnarray}
Var(\hat{\beta} ) = E[ (Cy)(Cy)^T] &=&\sigma^2 CC^T
\end{eqnarray}$$
ですが、\(C C^T \)を少し書き直します。\( C_{\ast} = (X^T X )^{-1} X^T \)とおいて、
$$\begin{eqnarray}
CC^T = ( (C-C_{\ast} ) +C_{\ast} )( (C-C_{\ast}) +C_{\ast})^T
\end{eqnarray}$$
と分解します。
\(CX=I \)を用いて、\( (C- C_{\ast} )X =0, (C- C_{\ast} )C_{\ast} =0 \)などが分かるので、
$$\begin{eqnarray}
CC^T =(C-C_{\ast} )(C-C_{\ast} )^T + C_{\ast} C_{\ast}^T
\end{eqnarray}$$
が成り立ちます。これから、\( \hat{\beta} \)の分散は、
$$\begin{eqnarray}
Var (\hat{\beta} ) &=&\sigma^2 ( (C-C_{\ast} )(C-C_{\ast} )^T + C_{\ast} C_{\ast}^T ) \\
&=& \sigma^2 ( (C-C_{\ast} )(C-C_{\ast} )^T + C_{\ast} C_{\ast}^T )
\end{eqnarray}$$
と計算出来ます。
第一項、二項共に正なので、分散は\(C=C_{\ast} \)の時に最小となります。10
また、計算すると、
$$\begin{eqnarray}
Var ( C_{\ast} y ) &=& \sigma ^2 (X^T X ) ^{-1}
\end{eqnarray}$$
が分かるので、任意の\( \hat{\beta} \)に対して、
$$\begin{eqnarray}
Var (\hat{\beta} ) \geq Var (C_{\ast} y )
\end{eqnarray}$$
が成り立ちます。これは、最小二乗法で求めた\( \hat{\beta} \)がBLUEである事を示しています。
なんと無しに使っていた最小二乗法は、ただ平均を通るように係数を決めているだけじゃないかと言われたりもしますが、ある意味で良い手法だったというお話でした。
この事実は、ガウス・マルコフの定理として知られています。
また、推定量の分散は、いくらでも小さくなるわけでは無い事が、今までの話から分かったと思います。分散の下限についての情報を与えてくれるのがFisher 情報行列です。解説した記事があるので、良かったら読んでみてください。

おまけ(BLUE になる過程を可視化する)
おまけとして、推定量がBLUEに落ち着いていくにつれて、推定量の分散が小さくなっていく実験を行います。
以下のような問題設定で行います。
\( \mathcal{N}(0,1 )\)からランダムに100個のデータ\(X_1 ,\cdots , X_{100} \)をサンプルする。このデータから、母分布(標準正規分布)の平均のBLUEを作る。
平均のBLUEは\( \bar{X} =\sum X_i /n \)です。
あえてパラメーター\(a_1 , \cdots , a_100 \)を用意して、推定量
$$\begin{eqnarray}
\hat{\mu } =\sum a_i X_i
\end{eqnarray}$$
を作ります。その次に、ラグランジュの未定乗数
$$\begin{eqnarray}
H= \sum a_i ^2 -\lambda (\sum a_i -1 )
\end{eqnarray}$$
を勾配法で \(a_i \)達についての勾配を取り、
$$\begin{eqnarray}
a’ = a – \eta \nabla _{a} H
\end{eqnarray}$$
で、パラメーターを更新していきます。
各ステップで、
$$\begin{eqnarray}
Var ( \hat{\mu} ) = \sum a_i ^2 + 2*\sum _{i>j} a_i a_j
\end{eqnarray}$$
も計算して、\(a_i \)の収束と分散\( Var ( \hat{\mu} ) \)を記録して、グラフを描きます。
最終的に、\( a_i = 1/100, Var(\mu) =1/100 , Bias(\mu )=0 \)に収束するはずです。
全コードはgithubを見てもらう事にして、データと結果だけを貼ります。
#データの準備
np.random.seed(3)
X=np.random.normal(loc=0,scale=1,size=100)
a = np.random.normal(size=100)
for i in range(2000):
a-=eta*nabla_MSE(a)
a_0.append(a[0])
V = Var(a)
var.append(V)
x_hat=a@X.T
bias.append(x_hat)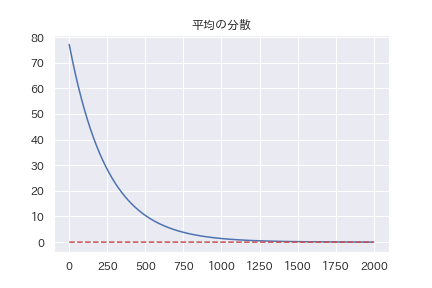
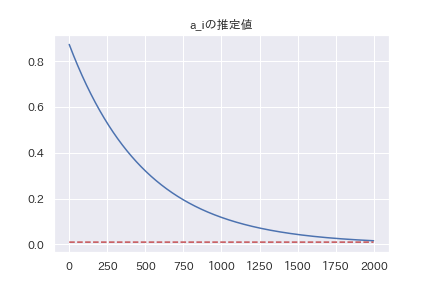
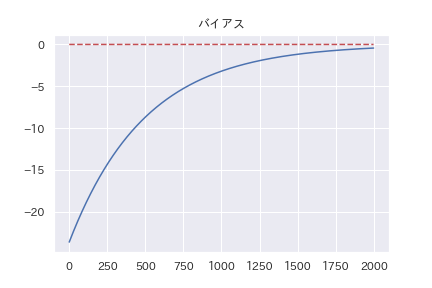
おおむね予想通りの結果になっています。
最終的な値を見ると、微妙にずれていたりするんですが、何故かは良く分かりません。
まとめ
- 不偏推定量の定義をした
- 平均値の例で、不偏推定量だから良いというわけでは無い事を説明した
- 推定量の分散を導入し、BLUEを説明した
- 最小二乗法は良いぞ
- BLUEになる様子を図にしてみた
- 最小二乗誤差
- フィッシャー情報量の記事にも同じような話が書いてます。
- 平均だけ決まってればどんな分布でも良いのですが。
- 普通の分散と同じですが。
- \(X_i \)達は正規分布に従うとします。
- ラグランジュの未定乗数法で出来ます。
- BLUE という文字列が格好いいので、いつか記事に書こうと思ってました。
- 現実で、不偏推定量で誤差を最小二出来るかは分からないですが。
- Iは単位行列です。
- 非負定値になるという意味で、大小を考えます。

