ワイブル分布を使って故障率を解析する

モノが壊れる時の統計の話の記事で、ワイブル分布の紹介をしました。この記事では、適当なデータに対してワイブル分布を当てはめて、故障率についての解析を行ってみます。

データはhttps://www.yukms.com/biostat/takahasi2/rec/004.htmにあるエクセルファイルの中のものを使わせてもらいました。一応、使ったデータはgithub に挙げておきます。

記事で使っているソースコードはgithub に置いてあります。
https://github.com/msamunetogetoge

データの確認
ワイブル分布の当てはめ
確率密度関数と故障率
ハザード関数
まとめ

データの確認

どんなデータか確認します。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt 
import seaborn as sns
import os
!pip install japanize-matplotlib
import japanize_matplotlib

df = pd.read_csv("wible_distlibution.csv")
df.columns = ['No', 't', '+']
df.head()

sns.distplot(df['t'],kde=False)
plt.title("使用データ")

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

import seaborn as sns

import os

!pip install japanize-matplotlib

import japanize_matplotlib

df = pd.read_csv("wible_distlibution.csv")

df.columns = ['No', 't', '+']

df.head()

sns.distplot(df['t'],kde=False)

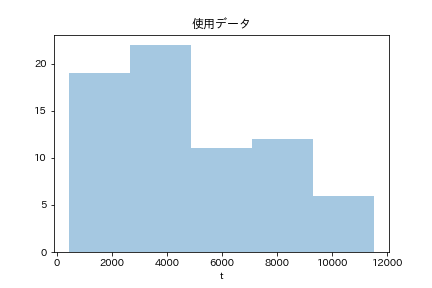
plt.title("使用データ")

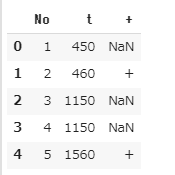
今回使うデータは、テストした製品の番号と壊れた時間、そして試験を打ち切ったかどうかの目印から構成されています。¹
\(t=4000 \)くらいまでには、大体が壊れるようですが、t=10000付近まで生き残るものもあり、寿命によって壊れているのか何か別の原因で壊れているのか、良く分からないデータです。
初めに、ワイブル分布を当てはめる為に、最尤法を使います。

ワイブル分布の当てはめ

ワイブル分布の確率密度関数を定義して、最尤法を行います。パラメーターは、良い感じの値から始めないと学習が進まないので、何かライブラリやソフトがあるなら、それを使った方が良いです。²

def weib(x,n,a):
    return (a / n) * (x / n)**(a - 1) * np.exp(-(x / n)**a)

def likly_food(x,n,a):
    return -np.sum(np.log(weib(x,n,a)))

lf_n = lambda n:likly_food(x,n,a)
lf_a = lambda a:likly_food(x,n,a)

h=1e-4 #微分の精度
n=1
a=0.1
eta=1e-6 #学習率
x=df["t"]
for i in range(10000):
    LF_old=likly_food(x,n,a)
    grad_n = (lf_n(n+h) - lf_n(n))/h
    grad_a = (lf_a(a+h)-lf_a(a))/h
    a+=eta*grad_n
    n+=eta*grad_a
    LF_new=likly_food(x,n,a)
    if i%50==0 and LF_new>= LF_old :
        print(i)
        print(f"a={a:.4f}")
        print(f"n={n:.4f}")
        break
        
    if i%1000 ==0:
        print(f"LF is {LF_new:.5f}")

print(f"a={a:.4f}")
print(f"n={n:.4f}")
#a=0.0965
#n=1.0113

def weib(x,n,a):

return (a / n) * (x / n)**(a - 1) * np.exp(-(x / n)**a)

def likly_food(x,n,a):

return -np.sum(np.log(weib(x,n,a)))

lf_n = lambda n:likly_food(x,n,a)

lf_a = lambda a:likly_food(x,n,a)

h=1e-4 #微分の精度

n=1

a=0.1

eta=1e-6 #学習率

x=df["t"]

for i in range(10000):

LF_old=likly_food(x,n,a)

grad_n = (lf_n(n+h) - lf_n(n))/h

grad_a = (lf_a(a+h)-lf_a(a))/h

a+=eta*grad_n

n+=eta*grad_a

LF_new=likly_food(x,n,a)

if i%50==0 and LF_new>= LF_old :

print(i)

print(f"a={a:.4f}")

print(f"n={n:.4f}")

break

if i%1000 ==0:

print(f"LF is {LF_new:.5f}")

print(f"a={a:.4f}")

print(f"n={n:.4f}")

#a=0.0965

#n=1.0113

それっぽいパラメーターが得られました。
aの値が1以上か否かで、故障の種類が分かれます。今回は、 a<1 なので、初期不良のデータっぽいです。つまり、時間が進むにつれて、故障のリスクが下がっていくような状況になっている事が予測できます。³
ちなみに、\(a=1 \)なら偶発的に故障が起きる状況、\( a>1 \) なら寿命で故障が起きる状況を表すと考えられます。⁴
次に、確率密度関数や累積分布関数を描きます。

確率密度関数と故障率

確率密度関数と、累積分布関数を描いてみます。

plt.plot(x, weib(x,n,a), label="確率密度関数")
plt.title(f"確率密度関数関数 a={a:.3f}, n={n:.3f}")
plt.legend()
plt.savefig("pdf_weib.png")

def weib_accum(x, n,a):
    return 1-np.exp(-(x/n)**a)

plt.plot(x, weib_accum(x,n,a), label="累積分布関数")
plt.legend()
plt.title(f"累積分布関数 a={a:.3f}, n={n:.3f}")
plt.savefig("cdf_weib.png")

plt.plot(x, weib(x,n,a), label="確率密度関数")

plt.title(f"確率密度関数関数 a={a:.3f}, n={n:.3f}")

plt.legend()

plt.savefig("pdf_weib.png")

def weib_accum(x, n,a):

return 1-np.exp(-(x/n)**a)

plt.plot(x, weib_accum(x,n,a), label="累積分布関数")

plt.legend()

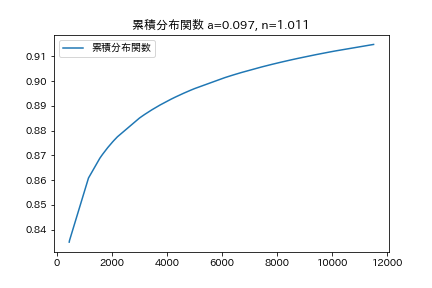
plt.title(f"累積分布関数 a={a:.3f}, n={n:.3f}")

plt.savefig("cdf_weib.png")

確率密度関数と。累積分布関数を見ると、tが小さい所で壊れるのが殆どで、tが大きい所ではそんなに壊れないという事が分かります。
これは、データがどのような試験の結果なのか分からないので何とも言えませんが、初期不良を検出するような試験だからなのかもしれません。累積分布関数が90%を超えるような時間を計算してみましょう。

X=np.linspace(1,10000,10000)
for x in X:
    if weib_accum(x,n,a)>0.9:
        print(x)
        break
#5711

X=np.linspace(1,10000,10000)

for x in X:

if weib_accum(x,n,a)>0.9:

print(x)

break

#5711

t=5711くらいで、故障率が90%を超えるようです。この数字が、故障が起きる目安となったりします。

ハザード関数

ハザード関数を計算し、壊れるリスクが時間によってどうなるのか見てみましょう。

def hazard(x,n,a):
    return (a/n)*x**(a-1)

plt.plot(x, hazard(x,n,a), label="ハザード関数")
plt.legend()
plt.title(f"ハザード関数 a={a:.3f}, n={n:.3f}")

def hazard(x,n,a):

return (a/n)*x**(a-1)

plt.plot(x, hazard(x,n,a), label="ハザード関数")

plt.legend()

plt.title(f"ハザード関数 a={a:.3f}, n={n:.3f}")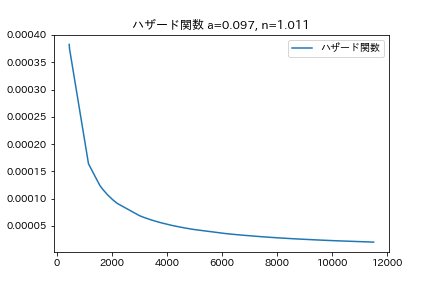

ハザード関数は、時間が経つにつれて、壊れる確率が減少する事を示しています。これは、生データが、t=4000までに大体が壊れてしまうのを反映した結果です。
ハザード関数を見ると、やはり初期不良を検出する為の試験を行ったのかもしれません。
そう思うと、上で計算された\( t=5711 \)という数字が初期不良が起きなくなる目安として捉える事が出来ます。
つまり、\(t>5711 \)の故障は、偶然に起きる故障か、寿命による故障ということです。逆に、\(t\leq 5711 \)での故障は、初期不良ということになります。

まとめ

ワイブル分布に当てはめる為に、最尤法を行った
確率密度関数や累積分布関数を描いた
ハザード関数を描いた
初期不良を検出する試験を行ったと推測できた
初期不良か否かを判定する時間を推定した

試験を打ち切った場合には、別の解析法がありますが、今回は、全て打ち切らずに壊せたと思って解析します。
ワイブル分布の場合は、少し式変形すると直線の式が出てくるので、そこからパラメーターを求めるというやり方もあります。wikiにやり方が載っています。
モノが壊れる時の統計の記事に貼ってある、バスタブ曲線を見てみてください。
ハザード関数が\( x^{a-1} \)に支配されている事を思い出してください。