ハザード関数とモデル選択の話

何かの製品が故障するまでの時間や、耐久性を予測したり、どの程度まで保証するか決めるというのは難しい問題です。統計的モデルを作る事で、正しいかは置いておいて、答えを出すことが出来ます。
初めに、確率変数を故障までの期間と考えると、故障率を確率の言葉で書けることを確認します。次に、ハザード関数を導入して、ハザード関数を指定する事で確率分布が決定されることを見ます。最後に、バスタブ曲線を表現しようと思うと、ワイブル分布が出てくることを解説します。
また、指数分布とワイブル分布どちらを使えば良いか分からない、という疑問に答えます。

参考文献は以下の本です。

Amazon.co.jp

故障率と信頼度
ハザード関数
バスタブ曲線の表現としてのワイブル分布
指数分布orワイブル分布?
まとめ

故障率と信頼度

何かが壊れるまでの時間などを確率変数だと思う事で、故障や破壊という現象を統計学の中に落とし込むことが出来ます。
確率変数を故障までの時間だとすると、累積分布関数$F_X (x) $ を時間xまでに製品が故障する確率と思う事が出来ます。
一方、$R(x) =1- F_X (x) $ は、時間xまで製品が壊れない確率と解釈できます。
確率変数$X $が故障に関する量を表すと考える時、$F_X (x) $を故障確率, $R(x) $を信頼度と呼んだりします。

故障確率を考える時に使う分布としては、指数分布、対数正規分布、ワイブル分布が代表的です。¹
指数分布とワイブル分布については、確率密度関数と故障率、信頼度を列挙しておきます。²
ただし、パラメーター$ \lambda , a, b >0$ で、確率変数の実現値xの取り得る値は0以上です。

[指数分布]

$$ \begin{eqnarray}
f(x|\lambda ) &=& \lambda \exp(-\lambda x ) \\
F(x) &=&1 -\exp(-\lambda x) \\
R(x) &=& \exp(-\lambda x)
\end{eqnarray}$$

[ワイブル分布]

$$ \begin{eqnarray}
f(x|a,b ) &=& abx^{b-1} \exp( -ax^b ) \\
F(x) &=&1 -\exp(-ax^b) \\
R(x) &=& \exp(-ax^b)
\end{eqnarray}$$

ある時間$x$ までに故障する確率を見ると、指数分布もワイブル分布も、xが大きくなれば故障率が上がるというのは一致しています。しかし、ワイブル分布の方が急激に故障率が大きくなることが分かります。つまり、ワイブル分布は、指数分布と比べて、ある瞬間に壊れていなくても、次の瞬間に壊れるか？という問いに、積極的にYes と答えます。
実際のデータに対して、これらを使う時には、最尤法などでパラメーターを決める事になります。その後、故障確率が90%や95% を超える点$x $を故障までの限界とする事があります。
しかし、指数分布とワイブル分布どちらを使うのが良いのか？という問題には、この情報だけでは答える事は出来ません。この問いに答える為に、ハザード関数という概念があります。

ハザード関数

故障確率を見る事で、ある時間までに故障している確率を見る事が出来ます。ある時間までは壊れずにいて、次の瞬間に壊れる確率を見る事も出来ます。
$X $を非負の連続型確率変数で、故障する時間を表しているとし、$f $を確率密度関数、$F$を累積分布関数とします。この時、xまで生きていて、その次の瞬間$x + \Delta x $までに故障する条件付確率は
$$\begin{eqnarray}
P(x <X\leq x+ \Delta x |X >x)
\end{eqnarray}$$
と書けます。これを少し変形しましょう。
$$\begin{eqnarray}
P(x <X\leq x+ \Delta x |X >x) &=& \frac{ P(x <X\leq x+ \Delta x , X >x)}{P(X >x)} \\
&=& \frac{F(x+\Delta x ) – F(x ) }{1-F(x)}
\end{eqnarray}$$
この両辺を$ \Delta x $で割って、$ \Delta x \rightarrow +0 $の極限を取る事で、$X=x $までは故障せずにいて、次の瞬間には故障している確率となります。
$$\begin{eqnarray}
\lim_{\Delta x \rightarrow +0}P(x <X\leq x+ \Delta x |X >x)
= \frac{f(x) }{1-F(x)}
\end{eqnarray}$$
この量の事を$ \lambda (x) $ と書いてハザード関数と呼びます。
ハザード関数から、確率密度関数も、累積分布関数も決まる事に注意しましょう。実際、ハザード関数を積分する事で
$$\begin{eqnarray}
\int _{0} ^{x} \lambda (t) dt &=& \int _{0} ^{x} \frac{f( t) }{1-F(t)} dt \\
&=& \left[ -\log (1-F(t) ) \right] _{0} ^{x} = -\log ( 1- F(t) )
\end{eqnarray}$$
となります。これから、
$$\begin{eqnarray}
F(x) &=& 1-\exp( – \int _{0} ^{x} \lambda (t) dt ) \\
f(x) &=& \lambda (x) \exp( – \int _{0} ^{x} \lambda (t) dt )
\end{eqnarray}$$
例えば、$ \lambda (x) =\lambda = $一定とすると、どんな時も確率$ \lambda $で故障する、という事象を表すモデルが出来ます。
上の式から計算すると、
$$\begin{eqnarray}
f(x) = \lambda (x) \exp( – \int _{0} ^{x} \lambda (t) dt ) = \lambda \exp ( -\lambda x )
\end{eqnarray}$$
となり、指数分布が出て来ます。つまり、いつ壊れるか良く分からない時は、指数分布から故障率などを計算しておけば良いということになります。

バスタブ曲線の表現としてのワイブル分布

製品の故障率を表すモデルとして、ハザード関数がバスタブ型のものが使われることがあります。品質管理とか品質保証系の人にはお馴染みのものかもしれません。
縦軸が故障率で、横軸が時間やストレスを表します。

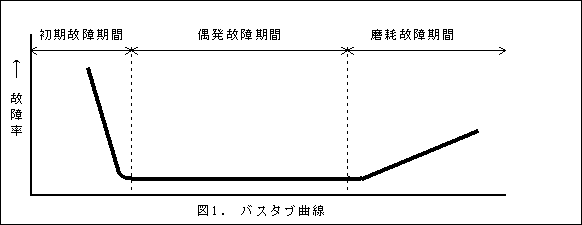
先ほど挙げた$ \lambda $ =一定のモデルは、画像のバスタブ曲線の偶発故障機関に当たります。³摩耗故障期間のように、時間が経つにつれて故障確率が上がるようなモデルとして、ワイブル分布が出て来ます。⁴

$ a, b >0 $として、ハザード関数を $ \lambda (x) =abx^{b-1} $としてみましょう。
$$\begin{eqnarray}
f(x) = \lambda (x) \exp( – \int _{0} ^{x} \lambda (t) dt ) = ab^a x^{b-1} \exp(-a x^b )
\end{eqnarray}$$
となり、ワイブル分布が出て来ました。ハザード関数の話を知っていると、パラメーター$ b$ が大きいと、壊れるのが速いモデルとなる事が直ぐに分かります。⁵時間によって、壊れる確率がどんどん上がっていくような現象に対しては、ワイブル分布を使っておくと良いという訳です。
ワイブル分布のパラメーターを推定して、故障までの期間や、耐えうるストレスを推定するというのがありますが、それは別の記事で解説します。

指数分布orワイブル分布?

使うモデルとして、指数分布がいいのか。ワイブル分布が良いのか？という問いに答えましょう。
時間の経過に対して、故障の確率は一定だという確信があれば、指数分布を使います。
時間の経過によって、故障の確率が急激にあがるなら、ワイブル分布を使います。
一方、ワイブル分布で、b=1とすると、指数分布になるので、いつもワイブル分布を使えば良いという気持ちにもなります。勿論、解析したい故障がどんな場面に居るのか分からないのであれば、取りあえずワイブル分布を使うのは良いと思います。しかし、現象が分からないから一般性の高いワイブル分布を使い、その結果を信用するのは危険だという事を胸に刻んでおくべきです。⁶

まとめ

故障率と信頼度を紹介した
ハザード関数という概念を導入した
ハザード関数から確率密度関数が決まる事を解説した
バスタブ曲線から、ワイブル分布が出てくることを解説した
指数分布とワイブル分布どちらを使えば良いか解説した

特に、ワイブル分布は色々な分布を表現したり、累積分布関数が簡単な形になる事から、よく使われます。
ワイブル分布から指数分布は出て来ますが、敢えて両方書きます。
製品設計の観点としては、初期故障で殆ど壊れて、保証期間後に摩耗故障機関が始めるようにする、みたいな話があります。
最初にワイブル分布が作られたのは、ハザード関数の話からでは無いのですが。ワイブルさんが物理的なモデルから作りました。解説してるブログがあるので興味が有ったら見てみてください。
もちろん、多項式より$exp $の方が強いので、ハザード関数の話を知らなくても分かります。
最尤法でパラメーターを求めた時に、厳密にb=0 となる確率は0なので、ほぼ確実に時間によって故障しやすくなるモデルが出来上がります。