EMアルゴリズムの簡単な応用として、ベイズ線形回帰1を考えましょう。ベイズ線形回帰と、EMアルゴリズムの記事は以下からどうぞ。


ベイズ線形回帰とEMアルゴリズム
ベイズ線形回帰では、\(t= w^{T} x + \epsilon \)の関係を仮定しました。ただし、\(\epsilon \)が誤差を表し、 \( p(\epsilon )= \mathcal{N} (0, \beta ^{-1} )\)とします。 2 次に\(w\) を確率変数だと思い、 正規分布\( p(w) = \mathcal{N} (w | m, S ) \)に従うと仮定します。
そして、既に持っているデータの情報を使って事後分布 \( p(w|t ) \)を求めました。
$$\begin{eqnarray}
p(w|t ) &=&\mathcal{N} (w|m_N , S_N )\\
S_N &=& S ^{-1} +\beta \sum x_i x_i ^{T} \\
m_N&=& S_N ( S^{-1} m + \beta \sum t_i x_i )
\end{eqnarray}$$
ここで、簡単の為に\( m=0 , S=\alpha ^{-1} I \)と置くと、
$$\begin{eqnarray}
p(w|t ) &=&\mathcal{N} (w|m_N , S_N )\\
S_N &=& \alpha ^{-1}I +\beta \sum x_i x_i ^{T} \\
m_N&=& S_N \beta \sum t_i x_i
\end{eqnarray}$$
となります。
EMアルゴリズムは未知の確率分布\( p(X| \theta ) \)を決める為に、隠れ変数\( Z \)を用意し、対数尤度を書き直しました。
$$\begin{eqnarray}
p(X|\theta ) = E_{Z}[p(X, Z|\theta ) ]
\end{eqnarray}$$
そして、KLダイバージェンスの性質を利用して最尤推定で\( \theta \)を求めたのでした。
\( p(w) = p(w|\alpha ) = \mathcal{N} (w | 0, \alpha^{-1}I ) \)と仮定していれば、
\( w\) を隠れ変数と思う事で、\(\theta = \{ \alpha , \beta \} \)を決める為にEMアルゴリズムを使う事が出来ます。
ベイズ線形回帰に対するEMアルゴリズム
まずはEMアルゴリズムの計算方法を確認しましょう。
[Eステップ]
1回目だけパラメーター\( \theta \)を初期化する。
$$\begin{eqnarray}
{\rm arg} \max _{q(Z)} \mathcal{L}(q, \theta ) \Leftrightarrow KL(q\| p ) =0
\end{eqnarray}$$
つまり、\(q = p(Z|X, \theta )\)とする。また、
$$\begin{eqnarray}
Q(\theta , \theta _{\rm old} ) &=& E_{p_{ \rm old}(Z) } [ \log p(X,Z| \theta ) ] \\
p_{ \rm old}(Z) &=& p(Z|X, \theta _{ {\rm old} } )
\end{eqnarray}$$
を計算する。
[Mステップ]
\( \theta \)で微分して、\( Q\)を最大化するためのパラメーターを求める。つまり、
$$\begin{eqnarray}
{\rm arg} \max _{\theta } Q(\theta , \theta _{\rm old} )
\end{eqnarray}$$
を行う。
ベイズ線形回帰の場合で考えると、\(X= t , Z=w , \theta = \{ \alpha , \beta \} \)です。
$$\begin{eqnarray}
p(X,Z|\theta ) &=& p(t, w|\alpha, \beta ) = p(t|w,\beta )p(w|\alpha ) \\
p(t|w, \beta ) &=& \prod \mathcal{N} (t_i | w^{T} x_i , \beta ^{-1} )\\
p(w|\alpha ) &=& \mathcal{N} (w|0, \alpha ^{-1}I ) \\
p(w|t, \alpha , \beta ) &=& \mathcal{N} (w| m_N , S_N )\\
S_N &=& \alpha ^{-1}I +\beta \sum x_i x_i ^{T} \\
m_N&=& S_N \beta \sum t_i x_i
\end{eqnarray}$$
を使って計算していきましょう。
$$\begin{eqnarray}
E&=&E_{p(w|t,\alpha , \beta )} [\log p(t, w|\alpha, \beta ) ]= \log p(t|w,\beta ) + \log p(w|\alpha ) \\
&=& \frac{N}{2}\log \frac{\beta}{\pi} -\frac{\beta}{2}\sum E [(t_i – w^{T}x_i )^2] \\
&+& \frac{M}{2} \log \frac{\alpha}{2} – \frac{\alpha}{2}E[w^{T} w]
\end{eqnarray}$$
ここで、
$$\begin{eqnarray}
E[w] &=& m_N \\
E[w^T w ] &=& E[ \rm{Tr} (ww^{T} ) ] = \rm {Tr} E[ww^{T} ] \\
&=&\rm{Tr} (m_N m_N ^{T} +S_N ) =m_N ^T m_N + \rm{Tr} S_N
\end{eqnarray}$$
に注意して微分を計算しましょう。
$$\begin{eqnarray}
\frac{\partial E}{\partial \alpha} &=& \frac{M}{2 \alpha} -\frac{1}{2}E[w^T w] \\
\frac{ \partial E}{\partial \beta} &=& \frac{N}{2\beta } – \frac{1}{2}\sum E [(t_i – w^{T}x_i )^2]
\end{eqnarray}$$
微分を0と置いて、期待値の計算を代入すると、パラメーターの更新式は以下になります。
$$\begin{eqnarray}
\alpha _{\rm {new} } &=& \frac{M}{ m_N ^T m_N + \rm{Tr} S_N } \\
\beta _{\rm {new} } &=& \frac{N}{ \sum \left( t_i -m_N ^{T} x_i)^2 + \rm{Tr} [x_i x_i ^{T} S_N ] \right) }
\end{eqnarray}$$
ただし、右辺の\( m_N , S_N \)に含まれる\(\alpha , \beta \)は更新する前の、古いパラメーターです。
ベイズ線形回帰に対するEMアルゴリズムをまとめると以下のようになります。
[Eステップ]
パラメーター\( \alpha , \beta \)で以下の量を計算する。
$$\begin{eqnarray}
S_N &=& \alpha ^{-1}I +\beta \sum x_i x_i ^{T} \\
m_N&=& S_N \beta \sum t_i x_i \\
E&=& E_{p(w|t,\alpha , \beta )} [\log p(t, w|\alpha, \beta ) ] \\
&=& \frac{N}{2}\log \frac{\beta}{\pi} -\frac{\beta}{2}\sum E [(t_i – w^{T}x_i )^2] \\
&+& \frac{M}{2} \log \frac{\alpha}{2} – \frac{\alpha}{2}E[w^{T} w] \\
\end{eqnarray}$$
ただし、
$$\begin{eqnarray}
E[w] &=& m_N \\
E[w^T w ] &=& E[ \rm{Tr} (ww^{T} ) ] = \rm {Tr} E[ww^{T} ] \\
&=&\rm{Tr} (m_N m_N ^{T} +S_N ) =m_N ^T m_N + \rm{Tr} S_N
\end{eqnarray} $$
[Mステップ]
以下の式に従って、パラメーター\( \alpha , \beta \)を更新する。
$$\begin{eqnarray}
\alpha _{\rm {new} } &=& \frac{M}{ m_N ^T m_N + \rm{Tr} S_N } \\
\beta _{\rm {new} } &=& \frac{N}{ \sum \left( t_i -m_N ^{T} x_i)^2 + \rm{Tr} [x_i x_i ^{T} S_N ] \right) }
\end{eqnarray}$$
対数尤度
$$\begin{eqnarray}
log p(t,w|\alpha , \beta ) =\log E_{p(w|t,\alpha , \beta )} [\log p(t, w|\alpha, \beta ) ]
\end{eqnarray}$$
を計算し、収束していれば終了し、収束していなければEステップに戻る。
python による実装
python でEMアルゴリズムで線形回帰してみます。上の式をカーネル化して使う3 を事も勿論できるわけですが、実装が面倒になるだけなのでそのままいきましょう。\(y=ax \)にノイズを加えたデータを生成し、EMアルゴリズムで\(a\)を推定します。
記事で使っているソースコードはgithub に置いてあります。
https://github.com/msamunetogetoge
1次関数だと味気ないので、3次関数の係数をEMアルゴリズムで解きましょう。式は
$$\begin{eqnarray}
y=a_0 + a_1 x + a_2 x^2 + a_3 x^3
\end{eqnarray}$$
です。
データを適当に準備します。
n=10
x=np.linspace(-10,10,n)
noize = np.random.normal(loc=0, scale=3,size=(n,1)).flatten()
y=10+3*x+5*x**2 + x**3
y=y+noize
df=pd.DataFrame(data=np.array([y,np.ones(len(x)), x, x**2 , x**3 ]).T, columns=["y", "const", "x", "x^2", "x^3"])
X=df[[ "const", "x", "x^2", "x^3"]]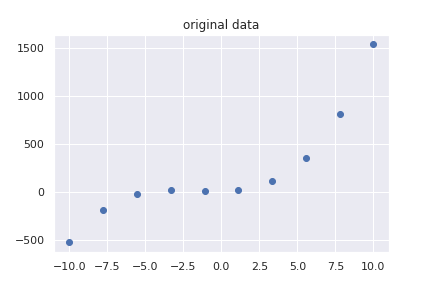
EMアルゴリズムを実装し、計算させます。4
M=len(X.columns)
em = EM_bayes(N=n,M=M )
[E,sigma,m]=em.Calc(X,y)
m=np.array(m).reshape(-1,M)
sigma = np.array(sigma).reshape(-1,M,M)\( a_0 \)の確率分布が収束していく5様をグラフに描いてみます。
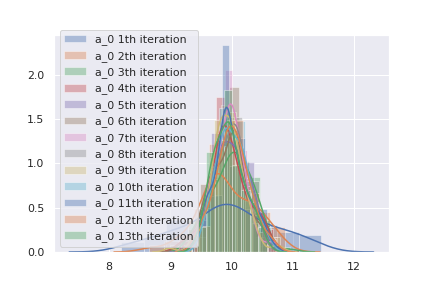
1回目の計算では、分散が大きいですが、計算が進むにつれてなんとなく尖った分布になっています。最終的に予測された確率分布から定数をサンプリングし、曲線を予測してみます。
[[a_0, a_1, a_2, a_3]] =np.random.multivariate_normal(mean=m[-1], cov=sigma[-1],size=1)
Y=a_0+a_1*x + a_2*x**2 + a_3*x**3
plt.plot(x,Y, label="predicted curve")
plt.scatter(x,y, label="original data", c="r")
plt.legend()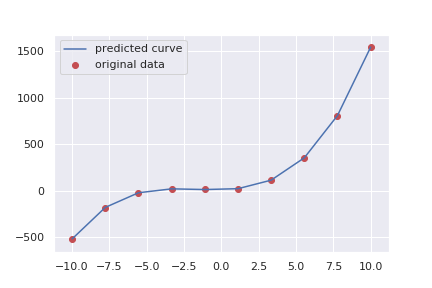
結構いい感じに予測することが出来ました。
まとめ
- EMアルゴリズムとベイズ線形回帰を復習した
- 線形回帰にEMアルゴリズムを適用するときの計算をした
- pythonで実装し、3次関数を求めた


