データが何かの分布に従うと仮定したら、パラメーターを求める為に何か計算をします。その時の手法として、最尤推定とベイズ推定1があります。それぞれの手法を比較し、注意するべき事を見つけます。
分散が既知の場合の、正規分布の平均値の推定を通して検証してみます。
ベイズ推定
ベイズ推定の手順を説明します。あるデータ\( (Y,X) \)があり、 \(Y=\{y_1 , \cdots , y_N \} \)は, 確率分布 \( y_n =p(x_n| \theta )\)に従うとします。この時、良い感じの \( \theta \) を決定すれば, \(X\)から\(Y \)が予想できる2という訳です。上手く\( p(\mu )\)を指定してやって、\( p( \mu |x ) \)が良く知っている確率分布になるようにしておくのが常套手段の1つです。\( p( \mu )\)が指定されていると、ベイズの定理から、 \(p(\mu |x ) \)が求められます。
$$\begin{eqnarray}
p(\theta |x ) = \frac{ p(x| \theta ) p(\theta)}{p(x)}
\end{eqnarray}$$
この記事の中では、パラメーターの事後分布を求める事をベイズ推定と呼びます。
右辺において、\( \theta \)に注目するのであれば、\( p(x) \)は定数であることに注意しましょう。
ベイズ推定の計算
同じ計算をするので、多次元正規分布を考えて、データの次元を1次元にして結果を使います。分散行列\( \Sigma \)は既知としましょう。 \( y_n = \mathcal{N} (x_n |\mu , \Sigma ) \)の場合を考えます。また、\( \mu \) も多次元正規分布に従うとします。
$$\begin{eqnarray}
p(\mu ) \sim \mathcal{N}(\mu _0 , \Sigma _0 )
\end{eqnarray}$$
\(\mu_0 , \Sigma_0 \)は人間が適当に与えてやります。今回はデータを無尽蔵に増やせるので、どんな値を与えても3上手くいきます。
今回の場合だと、\(p(\mu |X) \) は多次元正規分布になります。
\( p(\mu |X ) = \mathcal{N} ( \mu| \bar{\mu} , \Sigma _{\mu} ) \)と置いて、\( \mu \)について展開しておきます。
$$\begin{eqnarray}
\log p(\mu |X ) = -\frac{1}{2} \left[ \mu ^{T} \Sigma _{\mu} ^{-1} \mu -2 \mu ^{T} \Sigma _{\mu} ^{-1} \bar{\mu} \right] + {\rm const}
\end{eqnarray}$$
計算しやすいように\( \log \)を取ったベイズの定理を考えます。
$$\begin{eqnarray}
\log p(\mu |X ) = \log p(X| \mu ) + \log p(\mu )-\log p(X)
\end{eqnarray}$$
上で定義した確率分布を代入して、\(\mu \)についてまとめます。
$$\begin{eqnarray}
\log p(\mu |X ) = -\frac{1}{2}\left[\mu ^{T} ( N\Sigma ^{-1} + \Sigma _{\mu _0} ^{-1} )\mu -2\mu ^{T}( \Sigma ^{-1} \sum_{n}x_n + \Sigma _{\mu _0} ^{-1} \mu _0 ) \right] + { \rm const }
\end{eqnarray}$$
上の式と比べる事で、\( \mu \)が従う確率分布のパラメーターを求める事が出来ます。
$$\begin{eqnarray}
\Sigma _{\mu} ^{-1} &=& N\Sigma ^{-1} + \Sigma _{\mu _0} ^{-1}\\
\Sigma _{\mu} ^{-1} \bar{\mu} &=& \Sigma ^{-1} \sum_{n}x_n + \Sigma _{\mu _0} ^{-1} \mu _0 \\
\bar{\mu} &=& \left( N\Sigma ^{-1} + \Sigma _{\mu _0} ^{-1} \right) ^{-1} \left( \Sigma ^{-1} \sum_{n}x_n + \Sigma _{\mu _0} ^{-1} \mu _0 \right)
\end{eqnarray}$$
最尤推定の計算
正規分布の最尤推定については、以下の記事で解説しています。

結果的に、正規分布の平均値の最尤推定量は\( \bar{\mu} =\frac{1}{N} \sum x_n \)です。
python による実装
pythonで適当な正規分布を生成し、最尤推定、ベイズ推定それぞれで平均値を推定します。実験に使うコードを載せます。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
mu = 10
sig =5
Y = np.random.normal(loc=mu, scale=sig, size=100)
ys=[]
mu_ml=[]
fis=[]
mu_by=[]
lam =[]
for y in Y:
ys.append(y)
mu_ml.append(np.sum(ys)/len(ys) ) #最尤推定
fis=np.append(fis, sig**2 /len(ys) )
lam_by = len(ys)/sig+ 1/sig_zero
lam = np.append(lam,lam_by)
mu_by=np.append( mu_by,(np.sum(ys)/sig +mu_zero/sig_zero )/lam_by ) #ベイズ推定
plt.plot(mu_ml,label="Likelyhood")
plt.plot(mu_by, label="Byes")
plt.plot(10*np.ones(len(mu_ml)),c="r",lw=0.5)
plt.legend()
plt.ylim(5,15)
plt.title("Byes vs Lilelyhood")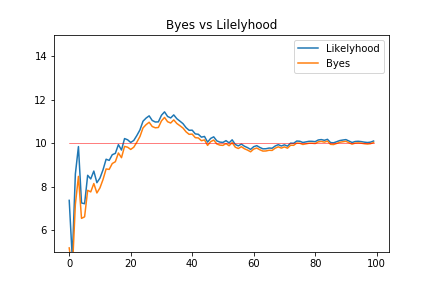
縦軸に推定された平均値、横軸に更新の回数を取ってグラフを描きました。
結果を見ると、ベイズ推定と最尤推定は殆ど同じ動きをしながらパラメーターを推定しています。
予測値の精度
予測の精度はどのくらいあるのでしょうか。
ベイズ推定なら\( \mu \)が従う正規分布の分散、最尤推定ならフィッシャー情報量の逆数が予測の精度の目安になります。フィッシャー情報量を知らない方は以下の記事をどうぞ。

正規分布の場合、平均値の最尤推定量の4分散は以下の式で下から抑えられています。
$$\begin{eqnarray}
{ \rm var }[\mu] \geq \sigma ^2 /N
\end{eqnarray} $$
この2つの目安を予測値の信頼度として、予測値のグラフに描き入れてみます。
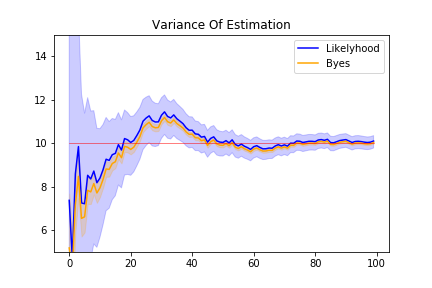
最尤推定の方が信頼度が小さく、ベイズ推定は最尤推定より精度が高い、という結果になりました。
ベイズ推定の場合は、\( \mu \)を計算しやすいように色々仮定を置いていました。その仮定の下では自信を持って予測しているという事です。
このことは、上手く現実を再現しているとは限らない事に注意しましょう。実際、繰り返しが20回未満では全く違う平均値を予測していますが、ベイズ推定の予測精度は高いことになっています。5ついでに書いておくと、事後分布の分散は、既知の分散\(\times \) データ数 と、人が設定した分散で決まるので、データ数が少ない場合は非常に恣意性が高くなります。
一方、最尤推定の誤差は、Fisher 情報量 (既知の分散/データ数)で下から抑えられています。更新をいくら続けても誤差が0になることはありません。その為、ベイズ推定より予測の精度が小さいという結果になっています。
今回の場合は、不偏推定量と最尤推定量が一致しているので、最尤推定を使っておけば良いということになります。
一般の場合では、最尤推定量が不偏推定量になるとは限らないのと、最尤推定の計算が出来るとは限らりません。ベイズ推定は、計算のしやすい仮定を置いたり、近似手法を使って計算を進める事が出来たりするので、難しい分布が出てくる問題にこそ、ベイズ推定が使えるかもしれません。
まとめ
- ベイズ推定の手順を説明した
- パラメーターをベイズ流で推定するときは、事後分布を手動で決める
- ベイズ推定は、上手く機能しているように見えても現実をうまく再現しているとは限らない
- 不偏推定量と最尤推定量が一致するなら最尤法
- 難しい分布の場合は色々近似の技があるベイズ推定


