ゼロから作るDeep Learning 2のRNN に関するコードを写経、解説していきます。お仕事で使う機会があったけど理解があやふやだったので、忘備録気味です。keras を使う際のパラメーターが何をするパラメーターか解説したいと思います。
今回は、シンプルなRNNそのものについてのお話です。参考書は以下です。
RNNとは?
大体の解説や、使い方は以下の記事を参考にしてください。

RNNとは、リカレントニューラルネットワーク(Recurrent Neural Network )の略語です。ニューラルネットワークの変種で、データ同士に関係があるという前提のモデルです。RNN層を計算グラフで描くと以下のようになります。
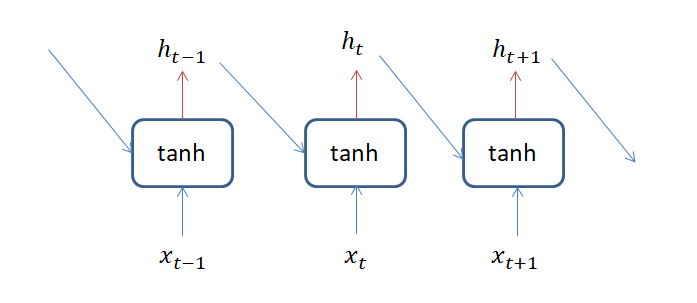
\(x_t \)が入力で\(h_t \)が出力です。大きな特徴は、出力\(h_t \)を入力 \( x_{t+1 }\)に加える事です。過去の情報を未来へ伝えていくイメージです。RNN層はそれ自体がモデルのような雰囲気がありますが、あくまで1つの層です。
RNNの実装
上に載せた計算グラフのようなモデルをpython で実装します。ニューラルネットワークとの違いは、活性化関数が\( \tanh \)である点と、過去の出力 \(h_{t-1} \)も全結合されている点です。誤差逆伝搬で必要な\( \tanh(x) =\frac{\sinh (x)}{\cosh (x) } \) の微分は以下のように計算出来ます。
$$\begin{eqnarray}
\tanh ^{,} (x)&=& 1- \sinh (x) \frac{ \sinh (x) }{\cosh ^2 (x) }\\
&=& 1-\tanh ^2 (x)
\end{eqnarray} $$
RNN層の時刻\(t \)の出力は以下の形をしている事に注意1 しましょう。
$$\begin{eqnarray}
h_t = \tanh \left(x_t W_{x_t} +h_{t-1} W_{t-1} +b_t \right)
\end{eqnarray} $$
それぞれの変数での微分は以下のようになります。
$$\begin{eqnarray}
\frac{\partial h_t}{\partial W_x} &=& \tanh ^{,} (x) \frac{\partial \left( x W_{x} +h W_{h} +b \right) }{\partial W_x} \\
&=& \tanh ^{,} (x) *x^{T} \\
\nabla _{x}h_t&=& \tanh ^{,}(x) \nabla _{x} \left( x W_{x} +h W_{h} +b \right) \\
&=& \tanh ^{,} (x) W_x ^{T} \\
\nabla _{b} h_t&=& \tanh ^{,}(x) \nabla _{b}\left( x W_{x} +h W_{h} +b \right) \\
&=&\sum \tanh ^{,}(x)
\end{eqnarray} $$
それではRNN層を実装します。ニューラルネットワークと殆ど同じ2 なので簡単です。
import numpy as np
class RNN:
def __init__(self, Wx, Wh, b):
self.params =[Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.cache = None
def forward(self, x, h_prev):
Wx, Wh, b = self.params
t = np.dot(h_prev, Wh) + np.dot(x, Wx) + b
h_next = np.tanh(t)
self.cache = (x, h_prev,h_next)
return h_next
def backward(self, dh_next):
Wx, Wh, b = self.params
x, h_prev,h_next = self.cache
dt = dh_next * (1- h_next **2)
db = np.sum(dt , axis= 0 )
dWh = np.dot(h_prev.T ,dt )
dh_prev = np.dot(dt, Wh.T)
dWx = np.dot(x.T, dt)
dx = np.dot(dt,Wx.T)
self.grads[0][...] = dWx
self.grads[1][...] = dWh
self.grads[2][...] = db
return dx, dh_prevこれでRNN層が実装出来ます。
ニューラルネットワークでも同様ですが、誤差逆伝搬では、後ろにある層から微分流れてきます。式で書くと以下のような状況になっています。本当の出力を\(O \)で表します。
$$\begin{eqnarray}
\nabla _{x} O= dh_{next}\nabla _{x} \tanh \left(x W_{x} +h W_{h} +b \right)
\end{eqnarray} $$
\(dh_{next} \)には色々な微分係数が入っています。
実際に使う際3には、勾配消失が起きる事を進歩居してバッチ学習をします。次は、バッチ学習が可能なRNNを実装しましょう。
バッチ学習用のRNN
例えば、\(t \)が\( 0\)から\(100000 \)まであるようなデータ\(x_t \)を一回で学習しようとすると、勾配が\(t=0 \)まで伝わる前に\( 0\)になってしまい、前半のデータの情報を学習に取り込むことが出来ません。
そこで、例えば\( t=10 \)毎にデータを区切って、それぞれに対して学習をします。ただし、区切るのは微分の情報だけで、順方向の情報はそのまま流します。
例えば、\(t=1000\)のデータで, 100個毎に区切り、バッチ数を2とすると、データを800個に分ける事になります。
$$\begin{eqnarray}
( x_0 , \cdots , x_9 ) \\
(x_{100} , \cdots, x_{109}) \\
\vdots\\
( x_{800} , \cdots , x_{809} ) \\
(x_{900} , \cdots, x_{999}) \\
\end{eqnarray}$$
この手法を TBTT(Truncated Backpropagation Through Time)と呼んだりします。
これをTimeRNN というクラスで実装します。
class TimeRNN:
def __init__(self, Wx, Wh, b):
self.params =[Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.layers = None
self.h = None
self.dh = None
def forward(self, xs):
Wx, Wh, b = self.params
N, T, D = xs.shape
D, H = Wx.shape
self.layers =[] #RNNたちのいれもの
hs = np.empty((N,T,H), dtype = "f")
self.h = np.zeros((N, H), dtype='f')
for t in range(T):
layer =RNN(*self.params)
self.h = layer.forward(xs[:,t,:], self.h)
hs[:,t,:] =self.h
self.layers.append(layer)
return hs
def backward(self, dhs):
Wx, Wh, b = self.params
N, T, D = dhs.shape
D, H = Wx.shape
dxs = np.empty((N,T,D), dtype="f")
dh = 0
grads =[0, 0, 0]
for t in range(T):
layer =self.layers[t]
dx, dh = layer.backward(dhs[:,t,:] + dh)#バッチ内で未来から勾配が流れてくるのでdhを足す
dxs[:,t,:] = dx
for i, grad in enumerate(layer.grads):
grads[i]+= grad #データが沢山あるので、それぞれの和がレイヤーとしての勾配になる
for i, grad in enumerate(grads):
self.grads[i][...] = grad
return dxs誤差逆伝搬が1つのバッチで完結していることに注目です。
次回の記事はこちら。
https://masamunetogetoge.com/makernn2
まとめ
- RNNの概要を説明した
- シンプルなRNN層を実装した
- 勾配消失を防ぐためのバッチ学習に対応したRNNを実装した
- 出てくる文字は出力と大文字以外はベクトルです。
- ニューラルネットワークの実装はこちらからどうぞhttps://masamunetogetoge.com/make-neuralnet-1
- そもそもこのようなシンプルなRNNは使われませんが



