EMアルゴリズムのpythonでの実装と一般化

混合正規分布に対するEMアルゴリズムの解説記事を書いたので、pythonで実装してみます。色んな人がやってるのでコードは見る必要が無いかもしれません。最後に、EMアルゴリズムの一般化について触れます。EMアルゴリズムの解説記事はこちら。

扱うデータが複数の分布を持っていそうな時、分布の混合割合と、パラメーターを推定する方法があります。それはEMアルゴリズムと呼ばれています。EMアルゴリズムの原理について解説します。

EＭアルゴリズムの復習
EMアルゴリズムのpython による実装
EMアルゴリズムの一般化
まとめ

EＭアルゴリズムの復習

解こうとしている問題の整理と、EMアルゴリズムの復習をします。
データ$ X =\{ x_1 , \cdots , x_n \} $に対するクラスター数$K $ の混合正規分布とは、以下の確率分布です。
$$\begin{eqnarray}
p(X) = \prod _n \sum_k \pi _k \mathcal{N}\left( x_n |\mu _k , \Sigma _k \right)
\end{eqnarray}$$
$ \mathcal{N}\left( x|\mu _k , \Sigma _k \right) $は多次元正規分布を表しています。$ \pi , \mu , \Sigma $を推定するのが目標です。
初めに、$ \pi $が隠れ変数$z$によってカテゴリー分布で表されているとして、$z$の事後分布$ \gamma (z) $ を求めます。
その後、対数尤度$L$を最大化する$ \pi , \mu , \Sigma $ を求めて、対数尤度がどのくらい更新されるか計算します。
殆ど更新されなければ処理終了です。大きく更新されていれば、新しいパラメーターで$ \gamma , \pi , \mu , \Sigma $を計算して尤度を計算しなおします。

[E ステップ]
$ \pi , \mu , \Sigma $ に適当な初期値を代入し、以下の量を計算します。
$$\begin{eqnarray}
\gamma(z_{nk}) &=&
\frac{ \pi_k \mathcal{N} \left( x_n| \mu _k , \Sigma _k \right) }{ \sum_j \pi_j \mathcal{N} \left( x_n| \mu _j , \Sigma _j \right) } \\
N_k &=& \sum_n \gamma (z_{nk} )
\end{eqnarray}$$

[M ステップ]
前に計算した量から、尤度と更新式を作ります。2回目以降は、以前の尤度と比較して、差が適当な数字$\epsilon $以下になったら更新を停止します。
$$\begin{eqnarray}
L&=&
\sum_n \log \sum_k \pi _k \mathcal{N} \left( x_n | \mu _k , \Sigma _k \right) \\
\mu _k &=& \frac{ \sum_{n} \gamma (z_{nk}) x_n }{N_k} \\
\Sigma _k &=&
\frac{1}{N_k} \sum_n \gamma (z_{nk} ) (x_n -\mu_k ) (x_n – \mu _k ) ^{T} \\
\pi_ k &=& \frac{N_k } {N}
\end{eqnarray}$$

以上の事を、python で実装してみましょう。

EMアルゴリズムのpython による実装

まずは学習させたいデータを作りましょう。楽をするために、1次元正規分布が混合されているとします。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

x1 = np.random.normal(loc=0.5, scale=1 , size =100).reshape(-1,1)
x2 = np.random.normal(loc=10, scale=2 , size =100).reshape(-1,1)
x3 = np.random.normal(loc=0, scale=3 , size =100).reshape(-1,1)
x = np.concatenate([x1 , x2 , x3])
sns.distplot( x )
plt.title("Gaussian Mixture Model")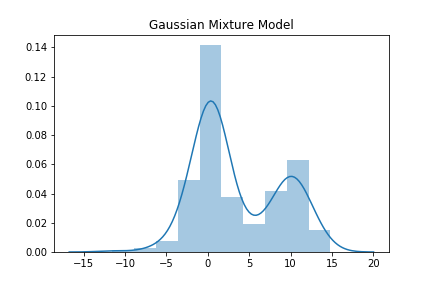

次に、各種値を計算するための関数を定義します。1次元の正規分布なのでnumpy が良い感じに計算してくれます。

def Gaus(x,m, s): #正規分布の値を取得
    g = np.exp( - pow((x-m), 2) /(2*s) )/np.sqrt(2*np.pi * s )
    return g

def calc_gamma(x, pi, mu, sig):#事後分布の計算
    gam = pi*Gaus(x,mu,sig)
    gam/= np.sum(gam, axis=1).reshape(len(x),1)
    return gam

def update_parmas(gamma, x, pi, mu, sig):#パラメーターの更新式
    N_k = np.sum(gamma, axis=0)
    N = np.sum(N_k)
    mu_k = np.sum(x*gamma, axis=0 ) /N_k
    sig_k = np.sum(gamma* pow(x-mu, 2), axis=0) /N_k
    pi_k = N_k/N
    return pi_k , mu_k, sig_k 

def iteration(x,mu,sig,pi, I=100, e=0.01):　#ε以下になるか、100回計算するまで尤度を更新する関数
    LF=0   
    for i in range(I):
        gamma = calc_gamma(x, pi, mu, sig)
        LF_new =np.sum(np.log(np.sum(pi*Gaus(x,mu,sig),axis=1 )) )
        ch = LF_new - LF
        print("LF ={} . change = {}".format(LF_new, ch))
        if np.abs(ch) < e:
            print("Iteration is finished {} iter. ".format(i+1))
            break
        LF=LF_new
        pi, mu, sig = update_parmas(gamma, x, pi, mu, sig)

    return pi, mu, sig

これらの関数を使って、適当な初期値を与えて計算してみます。今回は計算の上限は100回で、$\epsilon =0.01 $で行っていますが、適当で大丈夫です。

mu =np.array([0,10,3])
sig=np.array([1, 5, 10])
pi=np.array([0.1,0.4, 0.5])
pi, mu, sig = iteration(x,mu,sig, pi, I=100)
''''
LF =-892.8443809235707 . change = -892.8443809235707
LF =-840.4323250187838 . change = 52.41205590478694
LF =-832.8909016444818 . change = 7.541423374301985
LF =-830.0445451648682 . change = 2.8463564796136325
LF =-828.5494151559992 . change = 1.495130008868955
LF =-827.7057967180053 . change = 0.8436184379938823
LF =-827.2196118733798 . change = 0.4861848446255408
LF =-826.9346382849101 . change = 0.2849735884697111
LF =-826.761394736974 . change = 0.17324354793606744
LF =-826.650058986429 . change = 0.11133575054498124
LF =-826.5737961470172 . change = 0.076262839411811
LF =-826.5182732201362 . change = 0.055522926881053536
LF =-826.4757321464656 . change = 0.042541073670577134
LF =-826.4418517419456 . change = 0.03388040452000496
LF =-826.4141241860787 . change = 0.027727555866931652
LF =-826.391016011429 . change = 0.023108174649678404
LF =-826.371531020618 . change = 0.019484990810951786
LF =-826.3549798326762 . change = 0.01655118794178634
LF =-826.3408564862484 . change = 0.01412334642782298
LF =-826.3287709947581 . change = 0.012085491490324785
LF =-826.3184114191067 . change = 0.010359575651364139
LF =-826.3095216889953 . change = 0.008889730111377503
Iteration is finished 22 iter.
''''
print(pi, mu, np.sqrt(sig) )
#π [0.32736572 0.32643642 0.34619786] 
#μ [0.45400037  9.86360541 -0.01145557] 
#Σ [0.94493112 2.12668499 3.03373937]

初めに与えたデータは, $ \pi =(1/3, 1/3, 1/3) $ , $ \mu = (0.5, 10, 0) $, $ \Sigma = (1, 2,,3) $だったので、それなりには正しい答えを導けました。作った確率分布からサンプルしてグラフを描いてみます。

y0 = np.random.normal(loc=mu[0], scale=np.sqrt(sig)[0] , size =int(300*pi[0]) ).reshape(-1,1)
y1 = np.random.normal(loc=mu[1], scale=np.sqrt(sig)[1] , size =int(300*pi[1]) ).reshape(-1,1)
y2 = np.random.normal(loc=mu[2], scale=np.sqrt(sig)[2] , size =int(300*pi[2]) ).reshape(-1,1)
y=np.concatenate([y0, y1, y2])
sns.distplot(y)
plt.title("Predicted GMM")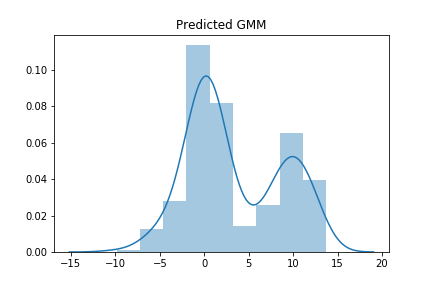

大体同じ形のグラフが書けたので、めでたしめでたしです。

EMアルゴリズムの一般化

別の記事の予告になりますが、イエンセンの不等式で、一般的な状況で(周辺化)対数尤度の評価が与えられます。 $p(X) $ を確率分布として、$Z $を隠れ変数としましょう。 $Z$ は確率分布$q(Z) $に従うとします。対数尤度の評価を与えます。
$$\begin{eqnarray}
\log p(X) &=& \log \int p(X,Z) p(Z)dZ \\
&=& \log \int q(Z) \frac{p(X,Z)}{q(Z)} dZ \\
&\geq & \int q(Z) \log \frac{p(X,Z)}{q(Z)} dZ = \mathcal{L}[q(Z)]
\end{eqnarray}$$
最後の$\mathcal{L}[\cdot ] $は汎関数のつもりで書きました。 $\mathcal{L}[\cdot ] $ は、$q(Z) $に関するELBO(evidence lower bound)と呼んだりします。
もう少し計算が進められます。
$$\begin{eqnarray}
\log p(X) – \mathcal{L}[q(Z)]&=& – \int q(Z) \left\{ \log \frac{p(X,Z)}{q(Z)} -\log p(X) \right\} dZ\\
&=& -\int q(Z) \log \frac{p(Z|X)}{q(Z)} dZ \\
&=&KL\left( q(Z) \| p(Z|X) \right)
\end{eqnarray}$$
対数尤度と、その下限の差は$p(Z|X) $を基準とした、 $q(Z) $とのKLダイバージェンスになっています。このKLダイバージェンスを監視して、EMアルゴリズムの更新をやめるかどうかを決めるという手法もあります。計算しやすい形に確率分布を近似する必要がありますが。別の記事でそのような話をしたいと思います。
確率分布の近似手法に平均場近似があります。その記事は以下からどうぞ。