Python でニューラルネットワークを実装してみましょう。前回は、データが与えられた時に0~9のラベルを出力する関数と、正解率を求める関数を実装しました。作ろうとしているモデルは以下のグラフで表されます。下の方に書いている小文字が、コードで使われる文字と対応しています。
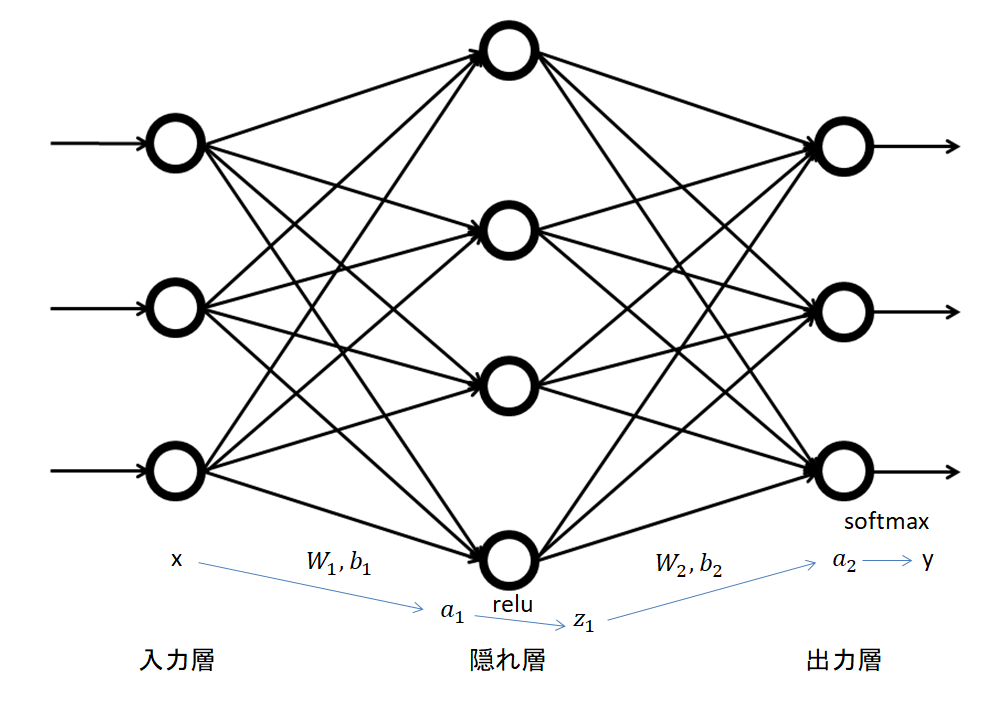
今回の目標は、誤差関数の計算と勾配の計算を行うことです。勾配が必要な理由や、計算の仕方については以下の記事をご覧ください。


記事で使っているソースコードはgithub に置いてあります。
https://github.com/msamunetogetoge
誤差関数(交差エントロピー)の実装
softmax 関数と、交差エントロピー誤差は以下の式で定義されます。
$$\begin{eqnarray}
L( \vec{y}, \vec{t} ) &=& – \sum t_i \log y_i
\end{eqnarray}$$
ラベルが2つの場合はロジスティック回帰で出てきました。
pythonでの実装コードは以下になります。ただし、ラベルがone hot encording 1 済みの場合は、正解ラベルに対応する成分だけ1なので、yの成分一つだけ取り出すという形で実装しています。
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
if t.size == y.size:
t = t.argmax(axis=1)
return -np.sum(np.log(y[np.arange(y.shape[0]), t] + 1e-7)) / y.shape[0]
誤差関数の計算をしてみましょう。0から10までの画像に対して計算します。計算できるという事が大事で、値の大きさは全く気にしません。
network=TwoLayerNet(input_size=len(train_images[0]),hidden_size=64, output_size=10)
y=network.predict(train_images[:10])
t=train_labels[:10]
cross_entropy_error(y,t)
#管理人の環境での出力 2.305356509113412関数の勾配の計算
関数の勾配 2 を計算しましょう。実装するには勾配の表式が必要です。softmax 関数と交差エントロピー誤差の合成の勾配を計算します。softmax 関数はfで表します。
$$\begin{eqnarray}
f(\vec{x} )&=& \left( \frac{\exp(x_1)}{\sum \exp(x_j)} , \cdots , \frac{\exp(x_N)}{\sum \exp(x_j)} \right) \\
L(\vec{y}, \vec{t}) &=& – \sum t_i \log y_i \\
\nabla L\left( f(\vec{x} ) , \vec{t} \right) _k &=&- \frac{ \partial}{\partial x_k } \sum t_i \left( x_i -\log \sum \exp(x_j ) \right) \\
&=& \frac{\exp(x_1)}{\sum \exp(x_j)} – t_k = f(x_k ) – t_k
\end{eqnarray}$$
ただし、ラベルのベクトルはone hot encordingされていると思っていて、\( \sum t_i =1 \)を使いました。ラベルは0~9の数字で表されていたので、one hot encording しておきます。
train_labels[0] #9
ohe = OneHotEncoder(sparse=False)
train_labels = ohe.fit_transform(train_labels.reshape(-1,1))
train_labels[0] #array([0., 0., 0., 0., 0., 0., 0., 0., 0., 1.]) relu 関数の微分は以下のようにしておきます。数学的には微分出来ない点がありますが、気にしないことにします。
$$\begin{eqnarray}
\frac{d}{dx} relu(x) = \begin{cases} 1 & (x \geq 0 )\\
0 & (x<0 )
\end{cases}
\end{eqnarray}$$
python コードは以下です。
def relu_grad(x):
grad = np.zeros(x.size).reshape(x.shape)
grad[x>=0] = 1
return gradモデルの勾配計算の実装
実装する必要のある計算を列挙します。
- 行列をベクトルに掛ける関数の,行列による微分
- 定数ベクトルを足す演算のベクトルによる微分
- relu の微分
- softmax 関数との微分
それぞれのパーツでの勾配を求めておけば、後はそれを掛けるだけです。例えば、出力層の\( y=f( W_2 x +b_2 )=f(X) \)における、\(b_2 \)の勾配は、 \( \frac{\partial X }{\partial {b_2}_k }=\vec{e}_k \)であることを使うと以下のように計算出来ます。ただし、\( \vec{e}_{k} \)は第k成分が1でそれ以外は0のベクトルです。
$$\begin{eqnarray}
\nabla_{b_2} L &=& \sum_{i} \frac{\partial L} {\partial X_i } \nabla_{b2} X_i \\
&=& \left( \frac{\partial L} {\partial X_1 } , \cdots , \frac{\partial L} {\partial X_N } \right) \\
&=& \vec{y} -\vec{t}
\end{eqnarray}$$
と計算出来ます。
その辺りがピンと来ない人は、以下の記事をご覧ください。

これで、勾配の実装をする準備 3 が整いました。 前の記事で定義したクラスに、次の関数を書き加えます。本当は先ほど定義したcross_entropy_error 関数を使っても良いのですが、計算途中のパラメーターが必要なので同じ意味のことを書いています。
def gradient(self, x, t):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
# 予測値の計算 (predict と同じ )
a1 = np.dot(x, W1) + b1
z1 = relu(a1)
a2 = np.dot(z1, W2) +b2
y = softmax(a2)
# 各ノードでの微分の計算。出力側から順々に計算する
batch_num = y.shape[0]
dy = (y - t )/ batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy,axis=0)
dz1 = np.dot(dy, W2.T)
da1 = relu_grad(a1) * dz1
grads['W1'] = np.dot(x.T, da1)
grads['b1'] = np.sum(da1,axis=0)
"""データを一つだけ渡したい時の関数
dy = y - t
grads['W2'] = np.dot(z1.reshape(-1,1), dy.reshape(1,-1))
grads['b2'] = dy
dz1 = np.dot(dy, W2.T)
da1 = relu_grad(a1) * dz1
grads['W1'] = np.dot(x.reshape(-1,1), da1.reshape(1,-1))
grads['b1'] = da1
"""
return grads前回作った適当な行列やベクトルで計算させてみましょう。
network=TwoLayerNet(input_size=784,hidden_size=84, output_size=10) #28*28=784
gr=network.gradient(train_images[0], train_labels[0])
print(gr["W1"].shape ) #(784, 64)
print(gr["b1"].shape )#(64,)
print(gr["W2"].shape )#(64, 10)
print(gr["b2"].shape )#(10,)上手く計算出来ているはずですが、エラーが出たら教えてください。
まとめ
・出力値から誤差関数を計算した。
・勾配を計算した。
・勾配は逆側から計算されるので、\(W_1 \) とかの誤差の計算を書き下そうとは思えない。
・python によるニューラルネットワークの実装➂はこちらから
https://masamunetogetoge.com/make-neuralnetwork3

