主成分分析を理解するための線形代数第四弾です。線形代数で一番大事(?)な概念である線形写像の固有値について解説します。前回までの記事の知識は持っていると仮定します。
前回の記事はこちら。

参考書は以下の書籍です。
固有ベクトルと固有値
今回の記事で出てくる線形写像は、\(f :V\rightarrow V \)となるような自分自身への線形写像とします。1
固有ベクトルとは、線形写像がベクトルの長さを変える\(a\)倍関数に見えるようなベクトルの事で、その\(a\) の事を固有値と言います。正確な定義を書きます。
\(f\) を\(V\)上の自己準同型とします。\(a \in K \)に対して、\(V\) の部分空間\(V_{a} =\ker (f-a) =\{f(x)=ax |x\in V \} \)を\(f \)が、\( V_a \neq 0 \)を満たすとき、\(a\)に属する固有部分空間と呼びます。固有部分空間の元を固有ベクトルと呼び、\(a\)を固有値と呼びます。
固有ベクトルや固有値の意味するところを考えてみましょう。
一つの固有値と固有ベクトルを固定します。固有ベクトルの意味するところは、\(K^{n} \)(例えば\( \mathbb{R} ^n \) )上で線形写像を行列表示したときに、軸方向に\(a\)倍する写像に見えるという事です。線形写像としては、0倍する線形写像が一番意味を持たないので、絶対値の大きい固有値と固有ベクトルの組が、線形写像\(f\) の特性を良く表していると考えられます。絶対値の小さい固有値に対応する固有ベクトルは、情報を殆ど捨ててしまう方向なので、\(f \)の情報を殆ど持っていないのです。
この考え方は、次のように主成分分析で使われています。固有値の絶対値を全て足し合わせた、約8割に達する固有値を選びます。次にその固有値に対応する固有ベクトルだけで行列を表現することによって、ノイズに近い余分な情報を捨て去ってしまいます。
行列式の定義と計算
線形写像\(f\)の固有値の計算を行うには、\(V_a \neq 0 \)となる\(a \in K \)を見つければ良いです。適当に基底を取ると線形写像は行列表示出来るという事と、以下の事実に注目すると、やるべきことが見えてきます。
\(A\in M_n (K) \) とします。以下は同値です。
- Aには逆行列が存在する。
- \( \det A \neq 0 \)
ただし、\( \det A \)は\(A \)の行列式です。
\( \ker (f-a) \neq 0 \)であることと、\( f-a \)が単射でないことが同値である事です。これは、\(f-a \)を行列表示した時、\( A-a \)が逆行列を持たないという事で、\( \det ( A-a)=0 \)という事です。 つまり、線形写像の固有値を得るには、行列式から\( a \)に関するn次多項式を得て、それを\(a \) について解けば良いのです。
固有値の計算のカギとなる行列式の定義や幾何学的意味について解説をします。
まずは定義と性質を見てみましょう。
行列に対して行列式\( \det : M_n (K) \rightarrow K \)を行列の次数に対して帰納的に定義します。\(M_{0}(K) =0 \)に対しては、\(\det 0 =1 \)とします。
\( A =\{a_{ij} \} \in M_n (K) \) とします。 \( i =1 , \cdots n \)に対して、\( A_i \in M_{n-1} (K) \) を、\(A \)から第n列と第i行を除いた行列とします。\(A \)の行列式\( \det A\)を以下で定めます。
$$\begin{eqnarray}
\det A = \sum (-1)^{n-i} a_{in} \det A_i
\end{eqnarray}$$
次数の低い行列に対して計算してみましょう。
\(a \in M_1 (K) \) とします。
$$\begin{eqnarray}
\det a = (-1)^{1-1} a \det 0 = a
\end{eqnarray} $$
このことから、1次元の行列(スカラー)に対しては恒等写像のように振舞う事が分かります。次は、2次正方行列の行列式を求めましょう。
$$\begin{eqnarray}
A=
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
\end{eqnarray} $$
の行列式を計算します。
$$\begin{eqnarray}
\det A=(-1)^{2-1}b\det c +(-1)^{2-2}da =ad -bc
\end{eqnarray} $$
となり、良く知っている形が出てきました。3次の行列も頑張って計算してみましょう。
$$\begin{eqnarray}
A&=&
\begin{pmatrix}
a & b & c\\
d & e & f \\
g & h & l
\end{pmatrix} \\
\det A &=& (-1)^{3-1} g \det A_1 + (-1)^{3-2} h \det A_2 + (-1)^{3-3} l \det A_3\\
&=& g(bf-ce)-h( af-cd) + l( ae – bd) \\
&=& bfg -gce -haf +hcd +lae -lbd
\end{eqnarray} $$
4次以上の行列だと手で計算する気が起きないですね。しかし、簡単に行列式が分かるような行列もあります。例えば、対角行列や、対角線より上側にだけ0以外の数字がある上三角行列は、行列式は、対角成分の積になります。
普通、教科書だとこの定義では理論的な計算にも不便なので、定義を書き直したりしますが、この記事ではそういう事は行わずに、行列式の幾何的な意味付けを簡単にするだけにしておきます。
2次の正方行列を考えましょう。行列を、縦ベクトルを2本横に並べたものだと考えてみます。
$$\begin{eqnarray}
v_1 =
\begin{pmatrix}
a \\
b
\end{pmatrix} , v_2 =
\begin{pmatrix}
c \\
d
\end{pmatrix}
\end{eqnarray} $$
この2つのベクトルが張る三角形の面積を求めてみましょう。これは幾何的なイメージで解くことが出来ます。画像を見てください。
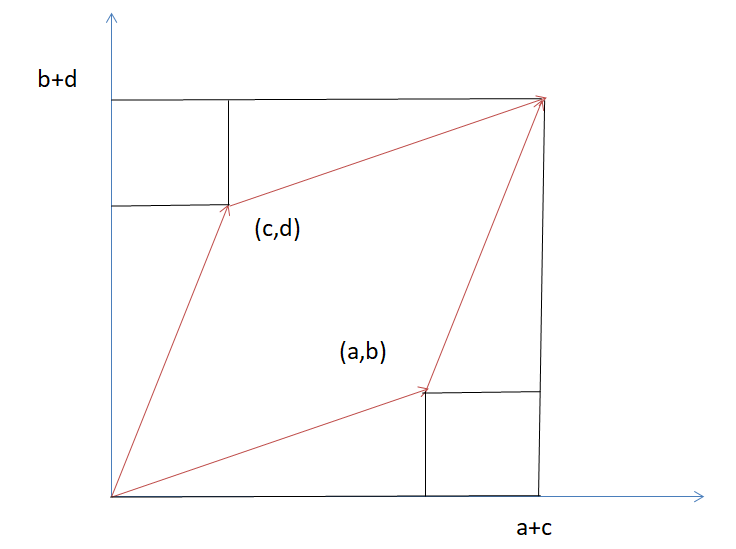
求めたい面積は赤線で囲まれた部分ですが、黒で囲まれた長方形や、赤と黒で囲まれた三角形は簡単に面積が求められます。全体の長方形から小さい長方形2つと三角形4つの面積を引きましょう。
$$\begin{eqnarray}
(a+b)(c+d) -2* b*c -c*d – a*b= ad-bc
\end{eqnarray} $$
2つのベクトルから作られる平行四辺形の面積 2 と行列式が一致していました。行列をベクトルから作られた量だと解釈することで、行列式は幾何学的な量だという事 3 が分かりました。
行列式は面積なので、回転や平行移動、鏡映に対して不変である4ことが分かります。基底を平行移動や回転に対応する線形写像で変換しても、行列式の値は変わらないのです。
固有値と行列式
結局固有値はどうやって計算したらいいのでしょう?
線形写像 \( f \) の行列表示を\( A \in M_n (K) \)としましょう。\(X \in M_n(K) \)で、対角成分に\( X\in K \)があり、それ以外は0である行列とします。以下の式を固有方程式 5 と呼びます。
$$\begin{eqnarray}
\det (X-A ) =0
\end{eqnarray} $$
この式は、Xについて高々\(n \)次の方程式 6 となるので、\(n\)次元線形空間の自己準同型の固有値は高々n個である事が分かります。いくつかの行列で固有値と固有ベクトルを計算してみましょう。
固有値の計算
適当な行列に対して、固有値を計算してみましょう。
[回転行列]
\( \theta \) だけ点を回転する行列を考えます。体は\(\mathbb{C} \) 7 とします。
$$\begin{eqnarray}
A&=&
\begin{pmatrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{pmatrix}
\end{eqnarray}$$
特性方程式を解きます。
$$\begin{eqnarray}
\det (X-A) &=& (X-\cos \theta )^2 +\sin \theta ^2 \\
&=& X^2 -2 \cos \theta X +1 \\
X_{\pm}&=& \cos \theta \pm i \sin \theta
\end{eqnarray}$$
固有値が分かりました。固有ベクトルの計算をしましょう。\(X_{+} \)についての固有ベクトルを求めます。以下の方程式から、\(x_1 , x_2 \)の関係を求めます。
$$\begin{eqnarray}
\begin{pmatrix}
i\sin \theta & \sin \theta \\
-\sin \theta & i \sin \theta
\end{pmatrix}
\begin{pmatrix}
x_1 \\
x_2
\end{pmatrix} =0
\end{eqnarray}$$
これから、\( x_1 = i x_2 \)が分かるので、固有ベクトルは、
$$\begin{eqnarray}
v_{+} =
\begin{pmatrix}
i \\
1
\end{pmatrix}
\end{eqnarray}$$
などがあります。\(X_{-} \)についても同様の事を考えてみると、
$$\begin{eqnarray}
v_{-} =
\begin{pmatrix}
-i \\
1
\end{pmatrix}
\end{eqnarray}$$
が分かります。教育的な理由で、以下のような計算をしてみましょう。
\(v_{+} , v_{-} \)の順で横に並べた行列
$$\begin{eqnarray}
P=
\begin{pmatrix}
i&-i \\
1&1
\end{pmatrix}
\end{eqnarray}$$
を考え、\( P^{-1} AP \)を計算してみます。
$$\begin{eqnarray}
P^{-1} AP &=& \frac{1}{2i}
\begin{pmatrix}
1&i \\
-i&1
\end{pmatrix}
\begin{pmatrix}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{pmatrix}
\begin{pmatrix}
i&-i \\
1&1
\end{pmatrix} \\
&=&
\begin{pmatrix}
\cos \theta+i\sin \theta & 0 \\
0 & \cos \theta -i \sin \theta
\end{pmatrix} \\
&=&
\begin{pmatrix}
X_{+} & 0 \\
0 & X_{-}
\end{pmatrix}
\end{eqnarray}$$
この計算から色々示唆が得られます。
- \( P^{-1}AP \)が左上から順に\(X_{+} , X_{-} \) と並ぶ。\( P \)を\(v_{-} , v_{+} \)で作ると\( X_{-}, X_{+} \) の順で固有値が並ぶ。
- 固有ベクトルを並べて作る行列\(P\)には逆行列がある。
- \( P^{-1} A P \)を計算すると、対角行列が出来るので、Aは固有ベクトルを基底として取った時の線形写像の表現行列になっている。従って、\( P^{-1}・P \)は線形空間で基底を変換する操作に対応する。
- 基底の変換をする線形写像は同型写像。
- 行列式は、固有値の積として計算できる。行列式が0である事と、固有値が0を含むことは同値。
以上述べた事は偶然でなく、線形代数の理論から導かれることです。面白いと思った方は教科書を買って読んでみましょう。
[微分を表現する行列]
2次までの実数係数多項式からなる線形空間
$$\begin{eqnarray}
P(X) =\left\{ a_0 +a_1 X + a_2 X^2 |a_0 , a_1 , a_2 \in \mathbb{R} \right\}
\end{eqnarray}$$
を考えましょう。基底として\( 1,X,X^2 \)が取れます。微分をする線形写像\(D: P(X) \rightarrow P(X) \)を各基底に対して以下のように定義しましょう。
$$\begin{eqnarray}
D(1)=0, D(X) =1,D(X^2) = 2X
\end{eqnarray}$$
この基底に関する表現行列は以下のようになります。
$$\begin{eqnarray}
A=
\begin{pmatrix}
0 & 1 & 0\\
0 & 0 & 2 \\
0 & 0 & 0
\end{pmatrix}
\end{eqnarray}$$
固有方程式 8 を考えましょう。
$$\begin{eqnarray}
\det (X-A ) =X^3
\end{eqnarray}$$
微分の固有値は0だけです。固有ベクトルは、例えば\( (1,0,1 )\) とかがあります。
固有値の数 \( \neq \) 行列の次数となるときは、全ての固有値に対して固有空間が存在するとは限りません。そのような時には、広義の固有空間を考えて、対角行列を作るのでなくて、特別な形の上三角行列 9 を作ります。 詳しい話は参考書を読んでほしいのですが、何回もかけると0 になってしまうベキ零行列と、有限次元性が大事な役割を果たします。
2次までの多項式なので、3回微分すると、全て0になってしまいます。表現行列を3回合成すると0になるので試してみてください。
まとめ
- 固有値の定義をした。
- 固有値は、固有方程式から計算できる。
- 固有方程式は行列式で定義される。
- 線形写像は、場合によっては対角行列に変換できる。
- そのような線形写像は\(V\) 上の自己準同型写像とか、単に自己準同型と呼ばれます。
- 正確には符号付の面積です。図で、ベクトルの上下を入れ替えると、\( bc-ad\) が答えとして得られます。
- 高次元の面積は体積という事にします。4次元以上の体積は、行列式の値で定義します。
- 意味をはっきりさせるには、回転や平行移動を行列で表す必要がありますが。実際、鏡映を施すと\( -1 \)倍されます。
- \( X- A \)という行列は、 \(X-f \)の行列表示である事に注意しましょう。
- 帰納法で簡単に証明できるので考えてみてください。
- \(\mathbb{R}\)で考えると、固有値なしになってしまいます。
- すでに上三角行列なので、計算しなくても固有値は0だけという事が分かります。
- ジョルダン標準形というやつです。


