主成分分析からカーネル主成分分析へ

良く分からないテーブルデータがある時、取りあえずデータの雰囲気を掴む手法の一つに、主成分分析があります。
線形代数の知識を使って主成分分析の原理を解説します。主成分分析の原理の理屈をそのまま使って、カーネル主成分分析 ¹ の解説をします。²
主成分分析の為の線形代数の記事は一通りあります。

線形空間(ベクトル空間)の解説

線形空間(ベクトル空間)についての解説記事です。線形代数が出来るうれしさを紹介した後、線形空間の定義、線形空間の例を紹介します。機械学習への応用についても少し触れています。

基底と線形独立性の解説

線形空間を知るためには、線形空間の元がどんなものか調べる必要があります。線形空間には、必ず0がありますが、他にも存在が保証される特別な元の組があります。それが基底です。基底の何が嬉しいか確認したのち、定義や例を紹介します。

線形代数の話(線形写像)

主成分分析を理解するための線形代数第三弾です。今回は線形写像について解説します。また、線形写像の行列表示について解説します。

線形代数の話(固有値と固有ベクトル)

線形写像の固有値と固有ベクトルについて解説します。いくつかの例に対して固有値と固有ベクトルを計算して、線形代数の理論に少しだけ触れます。

主成分分析とは？
特異値分解と主成分分析
カーネル主成分分析
カーネル主成分分析での実験
まとめ

主成分分析とは？

主成分分析とは、(一応)教師なし学習の一種です。適切な手法でデータの次元を小さくすることで、データの大体の傾向を掴むことが出来ます。ノイズに弱いデータを扱う場合や、データ全体の傾向を掴みたいとき、データをグループ分けしたい時に使う事があります。
主成分分析は、カーネル化が簡単にできます。カーネル化することで、複雑なデータも分類する事が出来ることもあります。スイスロールと呼ばれるデータの構造が良く例として出されます。³

スイスロール(クリックすると外部サイトに飛びます)

irisデータ⁴で大体どんな事が出来るか見てみましょう。説明変数4つと、花の種類からなるデータです。irisデータのグラフを載せておきます。

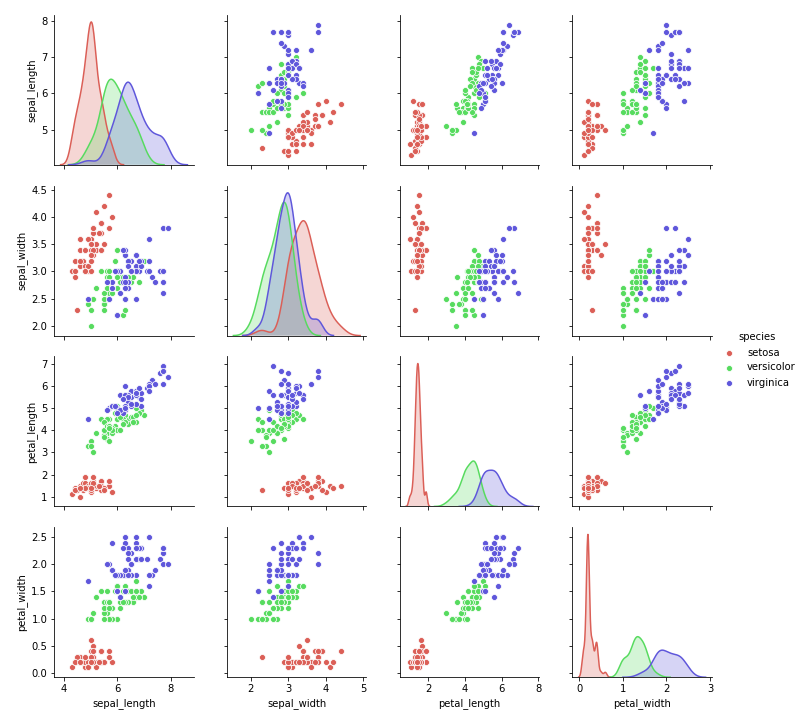
4つある説明変数を主成分分析によって2つにします。python だと一瞬で出来ます。
コードと実行結果を載せます。

import sklearn
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
import seaborn as sns

iris = sns.load_dataset('iris') #irisデータのロード

species = iris.pop("species") #ラベルは取り出しておく
pca = PCA(n_components= 2 ) #2次元に圧縮準備
pca.fit(iris)
iris_pca = pca.transform(iris)

iris_pca_pd = pd.DataFrame(iris_pca)#グラフを描く準備
iris_pca_pd["species"]= species
iris_pca_pd.columns = ["x0","x1", "species"]

sns.scatterplot(x="x0", y= "x1", hue="species", data=iris_pca_pd)
plt.title("PCA with iris data")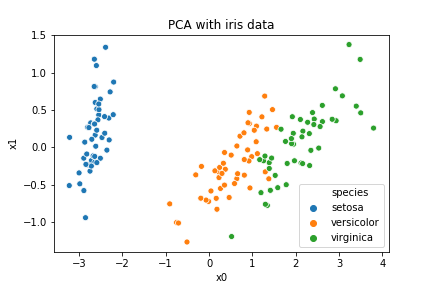

主成分分析で説明変数を2つにすることで、setosa とそれ以外を綺麗に分ける事が出来ました。元のデータが何種類の花のデータか分からなくても、少なくとも2種類のデータに分けられる事が分かりました。
このように、主成分分析を行う事でデータの大体の構造を見る事が出来ます。必ず一定の効果があるのが、主成分分析の強みです。主成分分析の原理と、そのカーネル化を説明していきます。

特異値分解と主成分分析

主成分分析は、与えられた行列の固有ベクトルを求め、好きな数の固有ベクトルで張られる空間に射影する手法です。絶対値の大きな固有ベクトルに対応する固有ベクトルを選ぶことで、行列の情報をあまり失わずに、大事な情報だけ取り出せるという算段です。
扱おうとしているデータをm次元ベクトルn個だと思いましょう。
$$\begin{eqnarray}
X = ( \vec{x_1 } , \cdots , \vec{x_n } )
\end{eqnarray} $$
行正方行列でないと固有値が考えられないので、自分自身との転置を取って正方行列にします。そのままのデータを使うのは出なくて、平均値からなる行列を引いて標準化します。
$$\begin{eqnarray}
\mu &=& \frac{1}{n} \sum \vec{x_i } \\
\tilde{X} &=& (\vec{x_1 } -\mu , \cdots , \vec{x_n } -\mu _m )
\end{eqnarray} $$
$ \tilde{X} \tilde{X} ^{T} , \tilde{X} ^{T} \tilde{X} $ それぞれの固有値を$\lambda _i , \mu _i $、固有ベクトルを $ u_i , v_i $ で表しましょう。
$$\begin{eqnarray}
\tilde{X} \tilde{X} ^{T} u_i &=& \lambda _i u_i \\
\tilde{X}^{T} \tilde{X} v_i &=& \mu _i v_i
\end{eqnarray} $$
左から $ \tilde{X} ^{T}, \tilde{X} $を掛けましょう。
$$\begin{eqnarray}
\tilde{X} ^{T} \tilde{X} \left( \tilde{X} ^{T} u_i \right) &=& \lambda _i \left( \tilde{X} ^{T} u_i\right) \\
\tilde{X} \tilde{X} ^{T} \left( \tilde{X} v_i \right) &=& \mu _i \left( \tilde{X} v_i\right)
\end{eqnarray} $$
$ m $ が小さい時は、固有値に対して固有ベクトルは定数倍を除いて一意なので、$ \lambda_i =\mu _i $です。同じ理由から $ \tilde{X} ^{T}u_i \propto v_i , \tilde{X} v_i \propto u_i $ です。比例係数は両者の大きさを比較して、次のように分かります。
$$\begin{eqnarray}
\| \tilde{X} ^{T} u_i \| ^2&=& \lambda _i \|u_i \| ^2 \\
\| \tilde{X} v_i \| ^2 &=& \lambda _i \| v_i \| ^2
\end{eqnarray} $$
固有ベクトルのノルムを1とすると、二つの行列の固有ベクトルは以下のように変換できることが分かります。
$$\begin{eqnarray}
\tilde{X} ^{T} u_i&=& \sqrt{\lambda _i } v_i \\
\tilde{X} v_i &=&\sqrt{ \lambda _i } u_i
\end{eqnarray} $$
$ \tilde{X} \tilde{X} ^{T} $ の相異なる固有値の数を$r \leq m$としましょう。正規直交基底⁵$ u_1 ,\cdots , u_r $を延長して新たな正規直交基底$u_1 , \cdots ,u_r , u_{r+1} , \cdots , u_m $を得る事が出来ます。同様に、$ v_1 , \cdots ,v_r , v_{r+1} , \cdots , v_m $ も作ります。基底の変換の式を、行列を使って一つの式にまとめます。
今できた基底を並べて2つの行列$U_m , V_m $が得られます。$U_m $ は$m\times m $行列、$V_m $は$n \times m $行列です。
$$\begin{eqnarray}
\Lambda ^{1/2} = \rm{diag} [ \sqrt{\lambda _1 }, \cdots , \sqrt{\lambda _r} , 0, \cdots ,0]
\end{eqnarray}$$
と置くと、以下の行列からなる方程式が得られます。
$$\begin{eqnarray}
\tilde{X} ^T U_m &=& V_m \Lambda ^{1/2}\\
\tilde{X}^{T} &=&V_m \Lambda ^{1/2} U_m ^{T}\\
\tilde{X} &=& U_m \Lambda ^{1/2} V_m ^{T}
\end{eqnarray} $$
最後の式を, $ X $の特異値分解 ⁶と呼びます。また、$ u_ i , v_i $の事を主成分と呼びます。
主成分分析とは、データの特異値分解を行い、固有ベクトルからなる空間にデータを射影する手法です。
普通は、固有値の和を求めておいて、大きい固有値から順に並べて固有値の和の8割を再現する個数の次元のデータに圧縮します。⁷次元をkに圧縮したい場合は、固有値を大きい順に並べて、対応する固有ベクトルから行列$ U_k= (u_1 , \cdots , u_k ) $を作り、データを射影します。つまり、
$$\begin{eqnarray}
U_k ^{T} (x_n – \mu )
\end{eqnarray} $$
を計算して、k次元のベクトルを得るということです。

カーネル主成分分析

カーネル主成分分析について説明します。
カーネル主成分分析は、一言で言えば主成分分析のカーネル化です。
カーネル法やカーネル化については以下の記事をどうぞ。

カーネル法入門

カーネル法の入門記事です。カーネル法を使うメリットデメリットを、回帰分析、カーネル回帰、カーネルリッジ回帰を例に出して簡単に、分かりやすく解説します。。

カーネル化

既存手法をカーネル法で扱う術について解説します。この記事の中ではカーネル化と呼びます。使うカーネルを決めるだけで、モデルの表現力を向上させることが出来ます。いくつかの例で実践してみます。

カーネル化を行うには、データからなる正方行列の部分をカーネル$K $に置き換えるだけです。
つまり、主成分分析の議論で出てきた、データから作った正方行列$\tilde{X} \tilde{X}^T $をカーネル$ K_{ij} = k (x_i , x_j ) $ で置き換えるのです。
主成分分析で出てきた、$ \tilde{X} = (\vec{x_1 } -\mu , \cdots , \vec{x_n } -\mu _n ) $と対応するカーネル$ \tilde{K} $は、中心化行列を使って作ります。
$$\begin{eqnarray}
H_n = I_n -\frac{1}{n} 1_n 1_n ^{T}
\end{eqnarray} $$
ただし、$I_n $はn次単位行列で、$1_n $は成分が1だけからなるn次元ベクトルです。$H_n$を中心化行列と呼びます。$H_n ^2 =H_n , H_n ^T =H_n , H_n X =\tilde{X} $となることが計算から分かります。
これを使って、
$$\begin{eqnarray}
\tilde{K} = H_n K
\end{eqnarray} $$
と置けば、$X $から$\tilde{X} $を作ったのと同じことになります。従って、解くべき固有値方程式は以下になります。
$$\begin{eqnarray}
H_n K H_n v = \nu v
\end{eqnarray} $$
データ$z $を主成分で表したいときは、
$$\begin{eqnarray}
\Lambda ^{-1/2}V_m ^{T} H k(z)
\end{eqnarray} $$
で計算出来ます。ただし、$k(z) $はベクトルで、第i成分は$ k(z)_i = k(x_i , z ) $で定義されます。⁸

カーネル主成分分析での実験

irisデータをカーネル主成分分析してみましょう。ガウスカーネルを使って、2次元のデータにしてみます。ガウスカーネルは、以下のように定義されるカーネルです。
$$\begin{eqnarray}
k(x,y) = \exp(-c \| x-y\| ^2 )
\end{eqnarray}$$
正規分布(ガウス分布)の主要部分と同じ形をしているので、ガウスカーネルです。⁹
コードと実行結果を書きます。¹⁰

import matplotlib.pyplot as plt
from sklearn.decomposition import KernelPCA
import seaborn as sns
Gam =[0.01, 0.1, 1]
plt.figure(figsize=(14,3))
for i,c in enumerate(Gam):
    plt.subplot(1,3, i+1)
    pca = KernelPCA(n_components= 2, kernel="rbf" ,gamma=c)
    iris_pca = pca.fit_transform(iris)
    
    iris_pca_pd = pd.DataFrame(iris_pca)
    iris_pca_pd["species"]= species
    iris_pca_pd.columns = ["x0","x1", "species"]
    sns.scatterplot(x="x0", y= "x1", hue="species", data=iris_pca_pd, )
    plt.title("Kernel PCA gamma={}".format(c) )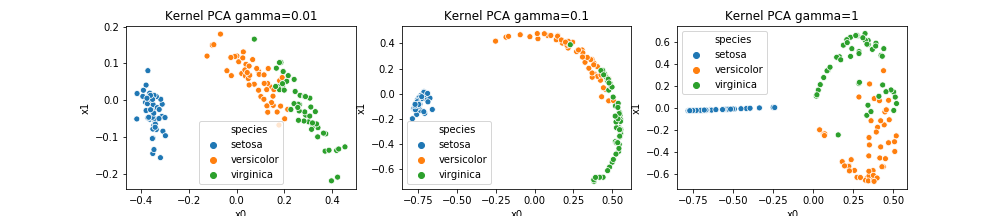

gamma=0.01 , 1の時がなんとなく3種類のデータになってると分かるでしょうか?カーネル法の非線形性によって、データが不思議な形に分布するのがカーネル主成分分析の特徴です。

まとめ

主成分分析を行う事で、データの持つ傾向を掴むことが出来る。
主成分分析=特異値分解$ \simeq $正方行列の対角化
主成分分析をカーネル化することで、カーネル主成分分析が出来る。
カーネル主成分分析を行うと、非線形なデータ構造を低い次元に射影出来る。

原理をそのまま使って、カーネル法の理論に移行する事を、カーネル化と言います。
カーネル主成分分析は、時と場合によっては異常検知や、分類問題にも使えます。
ロールケーキを縦において、横から見ると只の四角形ですが、実際には高さの次元を持っていて、上から見ると渦巻き状に見えるので、高さを考えると綺麗にデータを分類できるという話です。
irisデータとは3種類のアヤメを花の形によって分類したデータです。
対称行列の固有ベクトル同士は直交します。正規性はノルムで割ればいつでも得られます。
上の式変形では正規直交基底を並べて出来る行列が直交行列であることを使いました。
特異値分解で出てくる行列は、対称行列なので、固有値はいつも0より大きいです。
$x_i $は,i番目のデータです。
最もよく使われるカーネルです。
カーネル主成分分析を実装するのが面倒だったので、sklearn を使いました。すみません。