リッジ回帰分析 | マサムネの部屋

重回帰分析やニューラルネットワークは表現力が高く、過学習を起こしがちです。過学習を防ぐ方法の一つに、モデルにペナルティ項を加える方法があります。
今回はリッジ回帰と呼ばれる手法を紹介します。

リッジ回帰の利点
リッジ回帰の原理
リッジ回帰の注意点
リッジ回帰の効能
まとめ

リッジ回帰の利点

リッジ回帰の利点に、多重共線性があるデータでも加工なしに使える¹という点があります。また、パラメーター全部に同じペナルティを与えるので、モデルが過学習するのを防ぐことが期待できます。
以下で何故多重共線性がある場合でもデータの加工が不必要なのか見ていきます。

リッジ回帰の原理

リッジ回帰のモデルは、重回帰分析と同じですが、誤差関数に[mathjax]$L^2 $ 項のペナルティを課します。これを式で表してみます。
予測したい値からなるベクトルを[mathjax]$\vec{y}$ 、説明変数を平均で標準化したベクトルからなる行列を[mathjax]$X $ ² 、パラメーターからなるベクトルを[mathjax]$ \vec{ \beta} $と置きます。以下のような2乗誤差+ペナルティ項の形の誤差関数を考えます。
[mathjax]$$\begin{eqnarray}
S &=& \|\vec{y}- X \vec{\beta} \|^2 +\lambda \| \vec{\beta} \| ^2 \\
&=& ( \vec{y}- X \vec{\beta} )^{T} (\vec{y}- \vec{\beta} X)
+ \lambda \vec{\beta} ^{T} \vec{\beta}
\end{eqnarray}$$
$ \lambda \| \vec{\beta} \| ^2 (\lambda >0 ) $ の部分が[mathjax]$L^2 $項と呼ばれます。ベクトルは縦ベクトルだと思っています。$ \ \vec{\beta} ^{T} $はベクトルも行列だと思って、転置を表しています。
推定するべきパラメーターは[mathjax]$ \vec{\beta} $ です。[mathjax]$\lambda $ は人間が与えるパラメーターです。
多重共線性を消してくれる理由を考えていきます。最小二乗法でパラメーターを求めましょう。
[mathjax]$$\begin{eqnarray}
\nabla _{\vec{\beta}} S = -2X^{T} (\vec{y}- X \vec{\beta} ) +2\lambda \vec{\beta}
\end{eqnarray}$$
[mathjax]$ \nabla _{\vec{\beta}} S =0 $とおくと、[mathjax]$ \vec{\beta} $は以下のように解けます。
[mathjax]$$\begin{eqnarray}
\vec{\beta}= (X^{T} X + \lambda I)^{-1} (X^{T} \vec{y})
\end{eqnarray}$$
ここで、[mathjax]$ I$ はデータ数次元の単位行列です。[mathjax]$ \lambda =0 $とすると、重回帰分析を再現するという意味で重回帰分析の一般化になっています。重回帰分析では、多重共線性があると [mathjax]$ X^{T} X$ に逆行列が存在しないため、パラメーターを推定することが出来ませんでした。
リッジ回帰では [mathjax]$ \lambda $で固有値 ³ を0より大きくなるので逆行列が存在します。 ⁴ この点が、リッジ回帰は多重共線性があっても大丈夫と言われる所以です。もちろん、固有値が0に近い場合は逆行列が存在しても計算結果が不安定になるので注意が必要です。
データに多重共線性があるのでリッジ回帰を使いましょう、という安直な行動はあまり良くないことを以下で説明します。

リッジ回帰の注意点

リッジ回帰で多重共線性が解決できると書きましたが、それには注意が必要です。多重共線性を無視するためにリッジ回帰を行うのはどうかと思うわけです。一番良い多重共線性の取り除き方は、線形の関係にある変数を一つ取り除くことです。また、基本的に[mathjax]$ \lambda $ は小さい数字に取ります。固有値が確実に0より大きくなると言っても、0に近い事に変わらないので、パラメーターの推定という意味では不安定な解が出てきます。データ数が充分多い場合でない限り、多重共線性の存在を知っている場合は説明変数を工夫するべきでしょう。
多重共線性の存在について、もう一つ注意が必要です。多重共線性は、2変数間に限らないという事です。2変数間の多重共線性は相関係数やグラフを見れば分かりますが、3変数以上の場合はグラフを見たり、相関係数を見るだけでは分かりません。3変数以上の多重共線性は案外あります。例えば、何かの1g当たり含有量が説明変数になっている場合は、その何かを全て足せば1g になるので、いくつ説明変数があっても多重共線性を持ってしまいます。

リッジ回帰の効能

タイタニック号の生存者予測モデル(ニューラルネットワークモデル)にリッジ回帰のように[mathjax]$L^2 項$ を追加してみましょう。説明変数間の多重共線性はないので、純粋に過学習の抑制の効果を見てみたいと思います。過学習の抑制の効果をどう見るかですが、雑に何回パラメータを更新したときに、誤差関数の値が収束したかで判断したいと思います。雑ですが、実用上はそんな感じだと思います。基準にできる統計量などがあれば教えてください。タイタニック号の生存者データは以下のようになっていました。

初めに、ペナルティなしで学習させてみます。

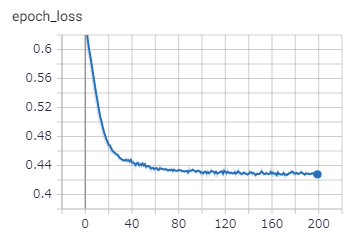
パラメーターの更新60回くらいで学習が進まなくなってるのが分かります。[mathjax]$ \lambda =0.1, 0.01 $として学習させてみます。(やばいほど過学習するデータで実験すればよかったと後悔しています。)

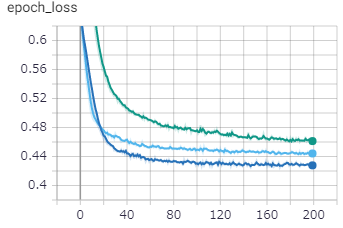
上から順に[mathjax]$ \lambda =0.1, 0.01 $ペナルティなしの学習結果です。
[mathjax]$ \lambda $を大きくすることで、学習のスピードが遅くなり、誤差関数の収束値が大きくなっていることが分かります。訓練用のデータを完ぺきに再現することは出来なくなっていますが、道のデータに対しては汎用性が上がっていると考えられます。

まとめ

・リッジ回帰のモデルは、重回帰モデル + [mathjax]$ L^2$項。
・ [mathjax]$ L^2$項に付随する[mathjax]$ \lambda $によって、多重共線性を緩和できる。
・取り除けるなら、多重共線性のある説明変数のどれかを捨てるのが一番良い
・タイタニック号の生存者データを使った実験は微妙だった。

多重共線性には、説明変数間に完全な線形の関係があって逆行列が求まらない場合と、線形の関係はあるが、誤差によって完全な線形関係にはなっていないが、逆行列を使った計算が不安定になる場合の2種類があります。機械学習で誤差関数を最小化するパラメーターを求めるという点ではどちらの場合も解決可能です。
[mathjax]$ X $は正方行列とは限らないが、 [mathjax]$ X^{T} X$はいつも正方行列になることに注意しましょう。
扱っている行列の固有値はいつも0以上です。
線形代数を知らないと意味不明だと思うので、行列の固有値に関する記事をいつか書きます。 https://masamunetogetoge.com/linearalg-eignvalue