尖度の解説~グラフから意味を読み取る~

尖度についての解説をします。正規分布と比べたときの裾野の重さを表す量と説明されたりします。また、確率分布の情報を知る為にモーメントを計算するわけですが、その一環として計算されたりもします。
この記事では、いくつかの確率分布に対して尖度を計算し、グラフを重ねて描く事で尖度が裾野の重さを表している事を確認します。

参考文献は定番の東大出版の本です。

Bitly

尖度の定義
正規分布の尖度
一様分布の尖度
ガンマ分布の尖度
グラフから尖度の意味を読み取る
1. パラメーターの調整
  1. 一様分布
  2. ガンマ分布
2. グラフの描画
まとめ

尖度の定義

確率分布の期待値を$ E[- ] $で表し、平均と分散を$ \mu , \sigma ^2 $で表します。尖度$ \alpha _4 $は以下の式で定義されます。
$$\begin{eqnarray}
\alpha _4 =\frac{ E[(X-\mu)^4 ]}{\sigma ^4 }
\end{eqnarray}$$
正規分布の尖度が3なので¹、正規分布を基準に考える為に、$\alpha _4 -3 $を定義に採用する事もあります。この記事では$\beta _4 $で表します。
$$\begin{eqnarray}
\beta _4 = \alpha _4 -3
\end{eqnarray}$$
$\alpha _4 $は、確率変数$X$の線形変換で不変です。²また、理論的に計算する時は、$X- \mu ^4 $を展開した以下の式を使う事もあります。
$$\begin{eqnarray}
\alpha _4 =\frac{ E[X^4] -4\mu E[X^3 ]+6\mu ^2 E[X^2 ] -3\mu ^4 }{\sigma ^4 }
\end{eqnarray}$$
尖度の意味としては、
$ (x-\mu ) ^4 $の値は、$x $が$ \mu $から離れると急激に大きくなるので、尖度が大きいという事は、$ \mu $より遠くの部分に殆ど値が分布していないことを意味する。そういう訳で、尖度が大きな確率分布は、尖ったような形を持つ。
というものがあります。³
何となくそういう気もしますが、納得するためにいくつかの例で計算してみましょう。⁴

正規分布の尖度

正規分布$ \mathcal{N} (\mu , \sigma ^2 ) $ の尖度を計算しましょう。
$$\begin{eqnarray}
E[(X-\mu)^4 ] = \int_{- \infty} ^{\infty} \frac{1}{\sqrt{2 \pi \sigma ^2 }} (x – \mu ) ^4 \exp( -(x-\mu )^2 /2\sigma ^2 ) dx
\end{eqnarray}$$
上の式で$ t= x-\mu $と変数変換して部分積分すると
$$\begin{eqnarray}
E[(X-\mu)^4 ] =\frac{1}{\sqrt{2 \pi \sigma ^2 }} \left\{ [- \sigma ^2 t^3 \exp( -t^2 /2\sigma ^2 )]_{- \infty } ^{\infty} + 3\sigma ^2 \int_{- \infty} ^{\infty}
t^2 \exp( -t^2 /2\sigma ^2 ) dx \right\}
\end{eqnarray}$$
ここで、第一項は0となり、第二項は、正規分布$ \mathcal{N}(0, \sigma ^2 ) $の分散の定義式なので、$ \sigma ^2 $となります。よって、
$$\begin{eqnarray}
E[(X-\mu)^4 ] =3\sigma ^4
\end{eqnarray}$$
です。これから、
$$\begin{eqnarray}
\alpha _4 &=& 3 \\
\beta _4 &=& 0
\end{eqnarray}$$
であることが分かります。任意の正規分布は、線形変換で標準正規分布に移ることで移りあえるので、尖度の中にパラメーターは出て来ません。
尖度の意味を理解するために、少し極端な分布の尖度を計算してみます。

一様分布の尖度

区間$ [a,b ] $上の一様分布の尖度を計算しましょう。一様分布は、$x\in [a,b ] $の時だけ値$1/(b-a) $を取る分布です。モーメントなどは、以下のようになります。⁵
$$\begin{eqnarray}
p(x)&=& \frac{1}{b-a} \\
E[X]&=& \frac{1}{2} (a+b) \\
\sigma ^2 &=& \frac{1}{12}(b-a)^2 \\
E[X^n] &=& \frac{1}{n+1}\sum_{k,l \geq 0 , k+l=n} a^k b^l
\end{eqnarray}$$
定義に従って尖度を計算すると、
$$\begin{eqnarray}
\alpha _4 &=& \frac{144}{80} = 1.8\\
\beta _4 &=& -1.2
\end{eqnarray}$$
となります。一様分布は、値が分布している場所なら、全て等確率なので、正規分布と比べて尖度は小さくなります。また、確率変数を線形変換すれば、どんな一様分布も作り出せるので、尖度にパラメーターは出て来ません。
最後に、パラメーターによって色々な形を取る事が出来るガンマ分布で尖度を計算します。

ガンマ分布の尖度

ガンマ分布の形や、モーメントは以下の式です。ただし、$a , b >0 $です。
$$\begin{eqnarray}
p(x|a,b ) &=& \frac{1}{\Gamma (a )} \frac{1}{b} \left( \frac{x}{b} \right)^{a -1 } e^{-x/ b }\\
E[X]&=& ba \\
\sigma ^2 &=& b^2 a\\
E[X^n] &=& b^n {}_{a+n -1}P_{n}
\end{eqnarray}$$
ただし、$ {}_{a+n -1}P_{n} = (a+n-1) (a+n-2 ) \cdots a $を表しています。定義に従って尖度を計算すると、
$$\begin{eqnarray}
\alpha _4 &=& 3+ \frac{6}{a} \\
\beta _4 &=& \frac{6}{a} (>0)
\end{eqnarray}$$
となります。ガンマ分布は、パラメーターを弄る事で色々な形を取る事が出来ますが、尖度が正規分布より小さくなることはありません。しかし、$ \alpha \rightarrow +\infty $の極限では正規分布の尖度と一致します。

グラフから尖度の意味を読み取る

今まで尖度を解析的に計算した確率分布(正規分布、一様分布、ガンマ分布)をグラフに描いて、尖度がどのようなものかを示してみます。
尖度は線形変換で不変なので、確率密度関数は色々な形になってしまいます。
その為、ある程度条件を揃える為に、平均1, 分散1となるようにパラメーターを調整します。⁶

パラメーターの調整

平均と分散を1に揃えるためのパラメーターの調整の計算を書いておきます。⁷

一様分布

一様分布の平均値と分散はパラメーター$a,<b$を使って
$$\begin{eqnarray}
\mu &=& (a+b)/2 \\
\sigma ^2 &=& (a-b)^2 /12
\end{eqnarray}$$
です。$a=-\sqrt{3} +1, b=\sqrt{3} +1 $とすれば、$\mu = \sigma ^2 =1 $となります。
この時、尖度は
$$\begin{eqnarray}
\alpha _4 &=& 1.8 \\
\beta _4 &=& -1.2
\end{eqnarray}$$
です。

ガンマ分布

ガンマ分布の平均値と分散はパラメーター$a, b$を使って
$$\begin{eqnarray}
\mu &=& ab \\
\sigma ^2 &=& ab^2
\end{eqnarray}$$
なので、$a=b=1 $とすれば $\mu = \sigma ^2 =1 $となります。
この時、尖度は
$$\begin{eqnarray}
\alpha _4 &=& 9 \\
\beta _4 &=& 6
\end{eqnarray}$$
です。

グラフの描画

上で調整したパラメーターで、確率密度関数のグラフを描きます。正規分布を使う場面では、平均±3分散で殆どのデータが取れるというのがあるので、$ \mu +3\sigma =4 $での値を比べる事で、裾野の重さを測定してみます。

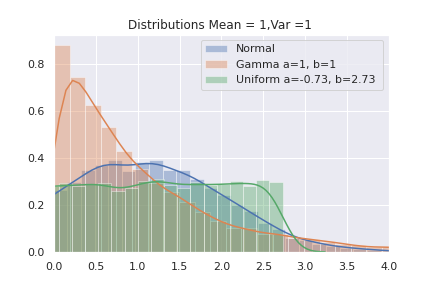
⁸グラフを見てみるとx軸の値が4.0の所では確率密度関数の値は
ガンマ分布>正規分布>一様分布
となっています。この順番は尖度の値の大きさの順番と一致しています。確かに、説明で使われるように、裾野の重さを表しています。
一方、最頻値や平均値回りの値でも、
ガンマ分布>正規分布>一様分布
となっています。平均値や最頻値周りで値を取りやすいかを判断する量としても使えそうです。