歪度(skewness)の解説をします。歪度を計算する事で、分布が平均に対して+,-側どちらに偏っているか判断できます。
参考文献は以下の2冊です。
歪度の定義
確率分布があるとき、期待値を\(E[\cdot ] \)で表します。また、平均、分散は\( \mu , \sigma \)で表します。
$$\begin{eqnarray}
\mu &=& E[X]\\
\sigma ^2 &=& E[ (X- \mu )^2 ]
\end{eqnarray}$$
歪度\( \alpha _3 \)は、以下の式で定義されます。
$$\begin{eqnarray}
\alpha _3 = E[ (X- \mu )^3 ]/ \sigma ^{3}
\end{eqnarray}$$
1歪度が0より大きいという事は、\(X > \mu \)の側に裾が長い事を意味します。逆もまた然りです。
正規分布の歪度
正規分布\( \mathcal{N} (\mu , \sigma ^2 ) \)は平均値に対して線対称な分布です。
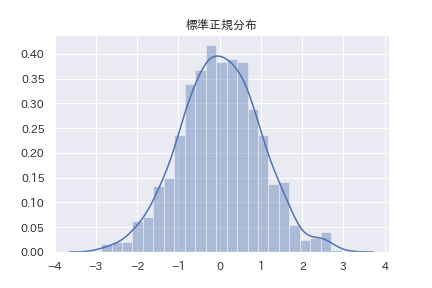
歪度の意味から考えると、正規分布の歪度は0であることが予想されます。これを確かめましょう。定義から、
$$\begin{eqnarray}
\alpha _3 &=& \int _{-\infty}^{\infty} (x-\mu )^3 \exp(-(x-\mu)^2 /2\sigma ^2 ) dx
\end{eqnarray}$$
ですが、\(x- \mu =t \)と変数変換すると
$$\begin{eqnarray}
\alpha _3 &=& \int _{-\infty}^{\infty} t^3 \exp(-t^2 /2\sigma ^2 ) dt
\end{eqnarray}$$
となります。上の式は奇関数を0で対称な区間で積分しているので0です。従って、正規分布の歪度は0であることが分かりました。
次に、分布が0付近で大きな値を取りやすい指数分布について歪度を計算してみましょう
指数分布の歪度
指数分布の表式と、平均値、分散は以下です。ただし、\(x>0 \)で定義されます。
$$\begin{eqnarray}
p(x|\lambda ) &=& \lambda \exp(-\lambda x )\\
\mu &=& 1/\lambda \\
\sigma ^2 &=& 1/ \lambda ^2
\end{eqnarray}$$
表式や平均値、分散を見ると、\(x=0 \)から急にそそり立つような、尖った分布になる事が分かります。この事から、\( \alpha _3>0 \)と予想出来ます。
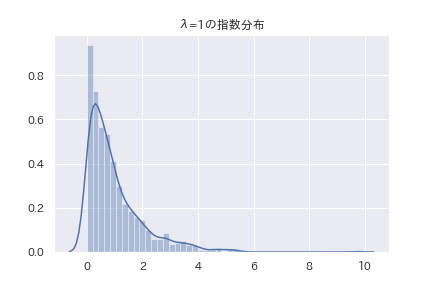
指数分布はガンマ分布の特別な場合で、特性関数や積率母関数が分かっているので、それを使って歪度が計算出来ます。2そのために、歪度の定義を少し書き換えます。
$$\begin{eqnarray}
\alpha _3 =\frac{ E[X^3] -3\mu E[X^2] +2\mu ^3 }{\sigma ^{3 } }
\end{eqnarray}$$
積率母関数は以下で与えられます。
$$\begin{eqnarray}
M_X (t) = (1- t/\lambda )^{-1}
\end{eqnarray}$$
2,3次のモーメントは
$$\begin{eqnarray}
E[X^2] &=& \frac{dM_X (t) ^2}{dt^2} |_{t=0} &=& 2/\lambda ^2 \\
E[X^3] &=& \frac{dM_X (t) ^3}{dt^3} |_{t=0} &=& 6/ \lambda ^3
\end{eqnarray}$$
と計算出来ます。\(E[X] =\mu = 1/\lambda \)と合わせて歪度の式に代入する事で、
$$\begin{eqnarray}
\alpha _3 =2
\end{eqnarray}$$
が得られます。予想通り、歪度は0より大きい値になりました。\(\lambda \)が小さくなれば、歪度も小さくなるような気もしますが、どんな\(\lambda _1 , \lambda _2 \)を取っても、 \(z= \lambda _2 / \lambda _1 x \)と線形変換すれば
$$\begin{eqnarray}
f(x|\lambda _1 ) = f(z|\lambda _2 )
\end{eqnarray}$$
と出来ます。線形変換で、歪度は不偏なので、指数分布の歪度は定数であることが分かります。
歪度と同様に定義される尖度という量もありますが、それは別の記事で解説したいと思います。
まとめ
- 歪度の定義をした
- 正規分布の歪度を計算した
- 指数分布の歪度を計算した


