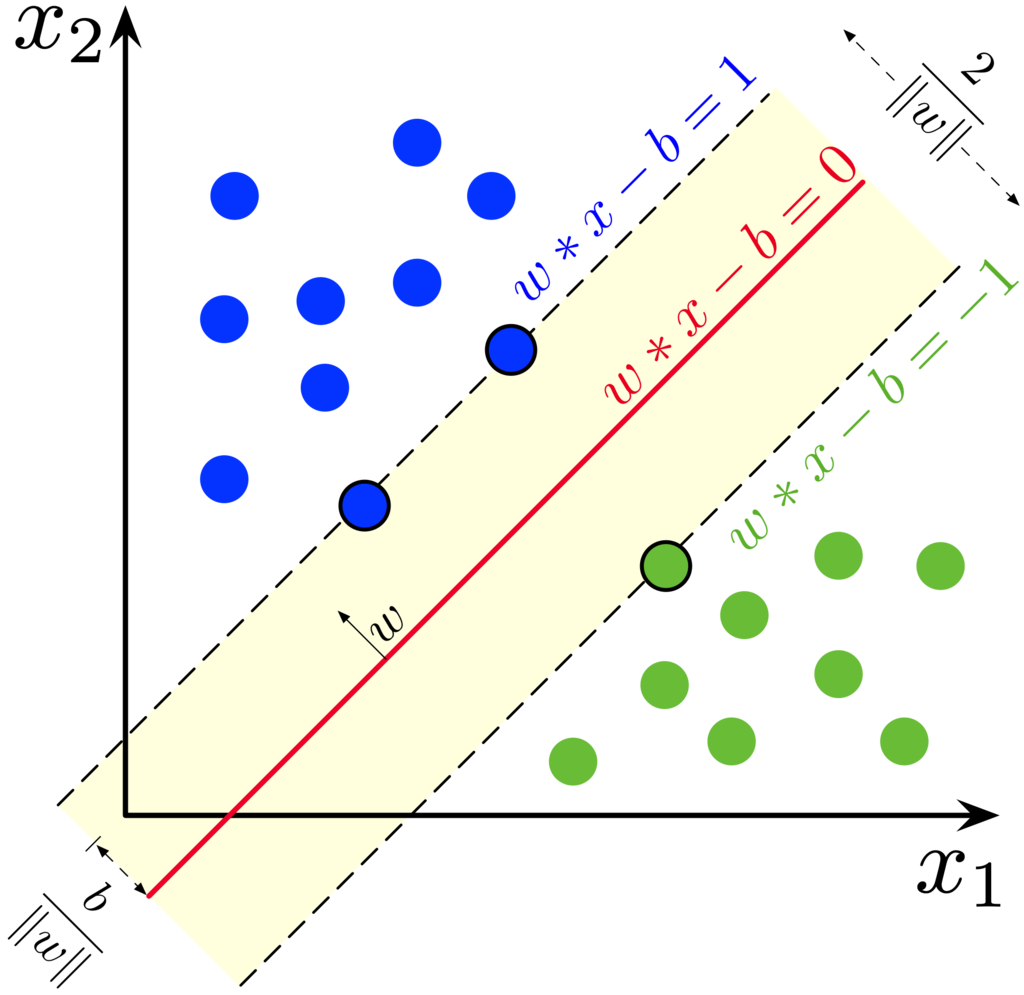
サポートベクトルマシンの幾何学的意味を解説します。
マージンと呼ばれる2つのデータ同士の距離を導入して、そこからサポートベクトルマシンの原理 1 を導きます。
また、サポートベクトルマシンをカーネル化することによって、非線形な関係のデータも分類できるようになります。それを確かめるために線形分離不可能で有名な、XOR 型のデータを分類してみたいと思います。
ハードマージンとソフトマージン
\( y=\pm 1 \)という2値分類問題に対して、以下の単純なモデルを考えましょう。
$$\begin{eqnarray}
f(x) =\vec{w} \cdot \vec{\phi (x) }
\end{eqnarray} $$
\( f(x)= \vec{w} \cdot \phi ( \vec{ x}) =0 \) と、\(\phi (x_i )\)の距離は以下で与えられます。
$$\begin{eqnarray}
d_i = \frac{ | \vec{w} ^{T} \cdot \phi (x_i )| }{ \| w \| }
\end{eqnarray} $$
\( d_ i \)の事をマージンと言います。マージンを出来るだけ大きくしようとするのがマージン最大化です。
全てのiに対して、
$$\begin{eqnarray}
y_i \vec{w}^{T} \cdot \phi (x_i ) \geq 1
\end{eqnarray} $$
を求めるのがハードマージンです。y=+1の時、大きな正の数字を返すか、y=-1の時に大きな負の数字を返せという条件式ですね。 2
これを課してしまうと、バリバリ過学習して役に立たないモノになってしまうので、少しだけ緩い条件にします。
$$\begin{eqnarray}
| \vec{w}^{T} \cdot \phi (x_i ) | \geq 1 -\xi _i
\end{eqnarray} $$
\( \xi _i \)をスラック変数と言い、この条件をソフトマージンと言います。
ところで、ハードマージンの場合でマージン最大化を式で以下のようになります。数学的に扱いやすいように\(L^2 \)ノルムで考えると、
$$\begin{eqnarray}
\arg_{ y_i \vec{w}^{T} \cdot \phi (x_i ) \geq 1 }\min \| \vec{w} \| ^2
\end{eqnarray} $$
となります。\( \arg_{hoge} \min \)というのはhoge という条件式で最小値を求めなさいという意味です。
ソフトマージンの場合は、\( y_i \vec{w}^{T} \cdot \phi (x_i ) \geq 1 – \xi _i \)という条件の下で、
$$\begin{eqnarray}
\arg_{ \vec{w} , \xi _i}\min \| \vec{w} \| ^2 + \lambda \sum \xi _i
\end{eqnarray} $$
となります。 \( w= \sum \alpha _i \phi (x_i ) \) と置くことで、誤差関数の最小化という観点から導出した式と同じ結果になります。
誤差関数からサポートベクトルマシンを導出する記事はこちらです。

モデルを以下のように書き換えて置くことで、全く同じ計算でカーネル化が行えます。既に持っているデータを\( ( (y_1 , x_1 ) , \cdots ,(x_n , y_n) )\)として、新たに予測したいデータを\( (y, x ) \)
$$\begin{eqnarray}
y=\sum alpha _i K(x_i ,x)
\end{eqnarray} $$
モデルのカーネル化についての解説記事はこちらからどうぞ。

サポートベクトルマシンによる分類
XOR 型のデータというのは,\(x*y \geq 0 \)なら1 , ,\(x*y <0 \) なら-1とラベル付けしたデータです。以下のような感じで、x=0 , y=0という2つの直線を使わないと分離可能な平面(直線)を作れないので、線形な関数では二つに完ぺきに分ける事が出来ません。
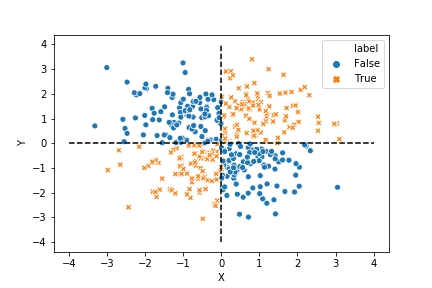
初めに、線形なサポートベクトルマシンで分類してみます。
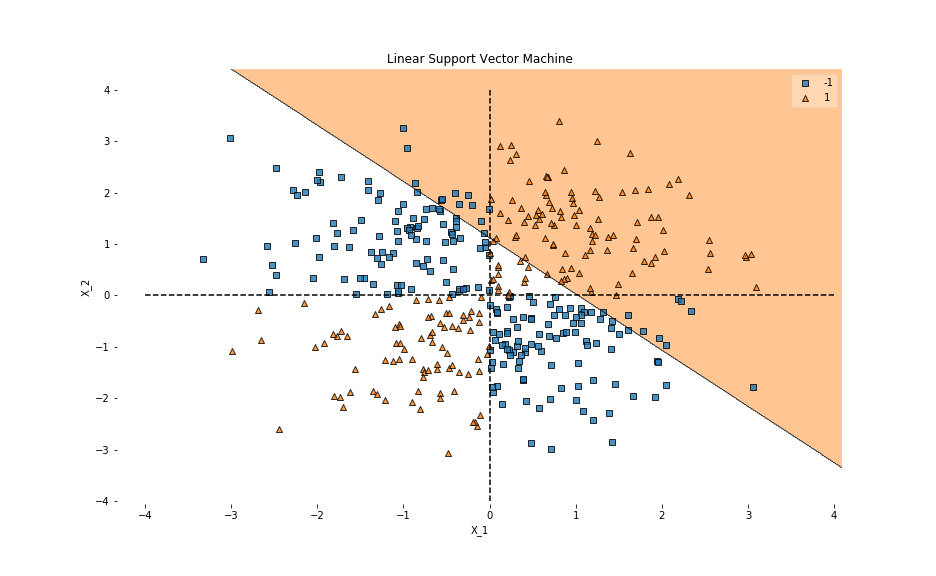
直線1本で頑張った結果、y=-xみたいな式で分離しました。上手くいかないのは当たり前なのですが、大事なのは線形関数での分類では絶対にうまくいかない問題があるという事です。次にRBFカーネルを使ってみましょう。
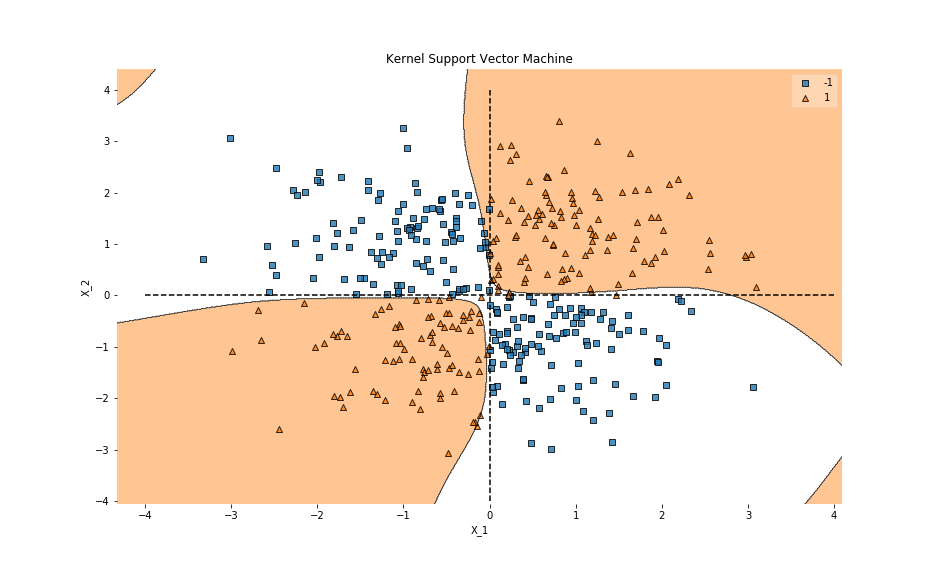
先ほどよりそれっぽく分類してくれています。今回のデータは\( y=x \) にノイズを載せて作ったデータでしたが、\(x<0 , y<0 \)の部分に分類の傾向が表れているような気がします。-1の領域に少しだけ+1の予測領域があるのが謎ですが、その辺はデータが無い場所なので仕方ないでしょう。大事なのは、線形ではうまくいかないけど、非線形ならうまくいく問題が有るという事です。
まとめ
・マージンというのは分離するために作った面同士の距離
・ソフトマージンを最大化するのがサポートベクトルマシン
・ソフトマージン最大化=ヒンジ関数を用いた誤差の最小化
・線形では2つに分離できない問題があるが、カーネル化する事で分類できるようになる。