大きな次元を持つデータ1 を小さな次元のデータで代替する方法の一つに主成分分析があります。それを確率論的に行う方法があり、ベイズ流に行う方法もあります。
確率論的に行う方法の記事が一応あるので興味があったら読んでください。
この記事では、参考文献の計算を追うのと、少しだけ発展的な計算もしてみます。
参考文献は緑本です。
確率論的主成分分析の設定
確率論的主成分分析を行う時の問題設定は以下のようなものです。
大きな次元Dのデータ\(y \)が、小さな次元Mのデータ\(x \)で生成されているとします。
そして、以下のように確率分布を設定し、パラメーターを決定するのが確率論的主成分分析です。
$$\begin{eqnarray}
x &\sim & \mathcal{N}(0,I )\\
y&=&W^T x+\mu + \epsilon \\
\epsilon &\sim & \mathcal{N} (0,\sigma ^2 I ) \\
p(y|x ) &=& \mathcal{N} (y| W^T x + \mu , \sigma ^2 )
\end{eqnarray}$$
\( \mu , W , \sigma ^2 \)がパラメーターです。
これら3つのパラメーターを決定するのが問題です。ここで、Dは取得したデータの次元ですが、Mは人が決める必要があります。2
平均場近似(変分推論)
ベイズの定理で事後分布を計算する際、解析的に計算出来ない事が多々あります。そんなとき、平均場近似を行う事があります。
$$\begin{eqnarray}
p(x_1 , \cdots , x_n ) \sim \prod_{i=1} ^{n}q(x_i )
\end{eqnarray}$$
KLダイバージェンスを最小にするには、\( q(x_i ) \)達は以下のように設定します。
$$\begin{eqnarray}
q( x_i ) = E_{x_{/i}}[p(x_1, \cdots , x_n , D) ] +const
\end{eqnarray}$$
ただし、\(p(x_1, \cdots , x_n , D) \)は取得しているデータ込みの同時分布で、\( E_{x_{/i}}[- ] \) は、\(x_i \)以外の変数で期待値を取るという意味です。3
ベイズ主成分分析1
ベイズ主成分分析では、\(x, \mu, \sigma ^2 , W \)に事前分布を設定し、データ\(Y \)を得た後の事後分布
$$\begin{eqnarray}
p(X,W,\mu , \sigma ^2 | Y)
\end{eqnarray}$$
を決定するのが問題になります。データYの次元がD.Xの次元がMで、M<D と設定すれば、データの次元を削減する事が出来ます。4
最初は、本に則って\( \sigma ^2 \)は人が与える事にして、
$$\begin{eqnarray}
p(X,W,\mu | Y, \sigma ^2 )
\end{eqnarray}$$
を推定する事を目標にします。また、計算の都合上、平均場近似して、
$$\begin{eqnarray}
p(X,W,\mu | Y, \sigma ^2 ) \sim q(X)q(W) q(\mu )
\end{eqnarray}$$
を仮定し、\(q(X), q(W) , q(\mu ) \)を推定する事を目標とします。
また、行列\(W \)については、M次元の独立な縦ベクトル\(W_d \)がD個集まっていると思います。
扱うモデルを組み立てましょう。
\(y \)が独立な\(W,X,\mu \)から生成されていると考えたいので同時分布は以下のように考えます。
$$\begin{eqnarray}
p(Y,X,W , \mu ) = p(W) p(\mu ) \prod_{n} p(y_n | x_n , W, \mu ) p(x_n )
\end{eqnarray}$$
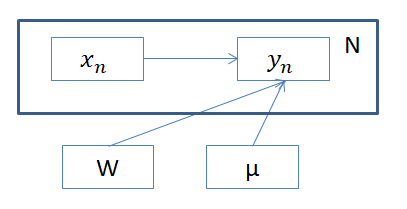
事前分布は、以下のように仮定します。5
$$\begin{eqnarray}
p(X)&=&\prod_{n} \mathcal{N} (x_n | 0, I_{M} ) \\
p(W) &=& \prod_{d} \mathcal{N} (w_d | 0, \Sigma _{W} )\\
p(\mu ) &=& \mathcal{N} ( \mu | 0, \Sigma _{\mu } )
\end{eqnarray}$$
平均場近似を使う場合は、以下のように\(q\)を決めると良いのでした。
$$\begin{eqnarray}
\log q(\mu )=E_{q(W)q(X)} [\log p(Y,X,W, \mu )] +const
\end{eqnarray}$$
\(q(W) , q(X ) \)も同じように決めます。出てくるのが全て正規分布なので、\(q(\mu ) , q(W) , q(X ) \)は全て正規分布になります。
計算結果は以下のようになります。
$$\begin{eqnarray}
q(\mu )&=&\mathcal{N}(q|\hat{m}_{\mu} , \hat{\Sigma}_{\mu} ) \\
\hat{\Sigma}_{\mu} ^{-1} &=& N/ \sigma ^{2} +\Sigma _{\mu} ^{-1} \\
\hat{m}_{\mu} &=& \frac{1}{\sigma ^2} \hat{\Sigma _{\mu}} \sum_{n} (y_n – E[W^t] [x_n] )\\
q(W) &=&\prod_{d} \mathcal{N}(W_d |\hat{m}_{W_d } , \hat{\Sigma}_{W} ) \\
\hat{\Sigma}_{W} ^{-1} &=& \frac{1}{\sigma ^2} \sum E[x_n x_n ^T ] +\Sigma_{W} ^{-1} \\
\hat{m}_{W_d } &=& \frac{1}{\sigma ^2} \hat{\Sigma}_{W} \sum_{n} (y_{n,d} – E[\mu _d])E[x_n ] \\
q(X ) &=& \prod_{n} \mathcal{N} (x_n | \hat{m} _{x_n} ,\hat{\Sigma } _{X} ) \\
\hat{\Sigma} _{X} ^{-1} &=& \frac{1}{\sigma ^2} \sum _{d} E[W_{d} W_{d} ^T ] +I \\
\hat{m} _{x_n} &=& \frac{1}{\sigma ^2} \hat{\Sigma} _{X} E[W](y_n -E[\mu] )
\end{eqnarray}$$
ただし、\(y_{n,d} ,\mu _d \)は、\(y_n , \mu \)の第d成分を表しています。計算の詳細は参考文献を見て欲しいのですが、全部同じように出来ます。一番書くのが簡単な\( \mu \)について、計算方法を書いておきます。
\( q(\mu ) \)の決定
$$\begin{eqnarray}
\log q(\mu )&=& E_{q(W)q(X)} [\log p(Y,X,W, \mu )] +const \\
&=& E_{q(W)q(X)} [ \log (p(W) p(\mu ) \prod_{n} p(y_n | x_n , W, \mu ) p(x_n )) ] + const \\
&=& \sum_{n} E_{q(W)q(X)} [ \log p(y_n | x_n , W, \mu ) ] +E[\log p(\mu ) ] + const
\end{eqnarray}$$
\( \mu \)についての関数なので、関係ない項は全てconstに吸収させています。\(E_{q(W)q(X)} [ \log p(y_n | x_n , W, \mu ) ] , E[\log p(\mu ) ] \)を計算しましょう。\(p(\mu ) \)は簡単です。
$$\begin{eqnarray}
E[\log p(\mu ) ] &=& -\frac{1}{2} \mu ^{T} \Sigma ^{-1} _{\mu} \mu
\end{eqnarray}$$
次に、\( \log p(y_n | x_n , W, \mu ) \)の期待値を取ります。
$$\begin{eqnarray}
E_{q(W)q(X)} [ \log p(y_n | x_n , W, \mu ) ] &=& E_{q(W)q(x_n )}[- \frac{1}{2\sigma ^2 } (y_n – ( W^T x_n -\mu ) )^T (y_n – ( W^T x_n -\mu) ] \\
&=& -\frac{1}{2} \left[ \mu ^T \mu / \sigma ^2 -2\mu ^T (y_n – E[W^T] E[x_n] ) \right] +const
\end{eqnarray}$$
nについて和を取って、それぞれを足し合わせると
$$\begin{eqnarray}
\log q( \mu ) =-\frac{1}{2}\left( \mu ^{T} (N\sigma ^{-2} I + \Sigma ^{-1} _{\mu } ) \mu -2 \mu ^T (y_n – E[W^T ] E[x_n ] ) \right) +const
\end{eqnarray}$$
となります。\(\mu \)についての二次式なので、\(q( \mu ) \)が正規分布になることが分かります。まとめると以下のようになります。
$$\begin{eqnarray}
q(\mu )&=&\mathcal{N}(q|\hat{m}_{\mu} , \hat{\Sigma}_{\mu} ) \\
\hat{\Sigma}_{\mu} ^{-1} &=& N/ \sigma ^{2} +\Sigma _{\mu} ^{-1} \\
\hat{m}_{\mu} &=& \frac{1}{\sigma ^2} \hat{\Sigma _{\mu}} \sum_{n} (y_n – E[W^t] [x_n] )
\end{eqnarray}$$
\(q \)の中には、期待値が含まれていますが、初期値を与えていれば近似分布\(q \)たちは定まっているので、計算が出来ます。
$$\begin{eqnarray}
E[\mu] &=& \hat{m}_{\mu} \\
E[W_d] &=& \hat{m}_{W_d} \\
E[W_d W_d ^{T} ] &=& \hat{m}_{W_d} \hat{m}_{W_d} ^T +\hat{\Sigma }_{W} \\
E[x_n ] &=& \hat{m} _{x_n } \\
E[x_n x_n ^T] &=& \hat{m} _{x_n } \hat{m} _{x_n } ^T + \hat{\Sigma} _{X}
\end{eqnarray}$$
近似分布の更新と、期待値の計算を繰り返す事で、モデルを学習していく事が出来ます。
ベイズ主成分分析2
上の計算では、\( \sigma ^2 \)は人間が与えていました。\(\sigma ^2 \)も推論で決められるようにガンマ分布に従うと仮定してみましょう。
$$\begin{eqnarray}
p( \sigma ^{-2} ) = { \rm Gam }( \sigma ^{-2}|a,b) = C (\sigma ^{-2})^{a-1} \exp(-b\sigma ^{-2} )
\end{eqnarray}$$
\( \log \)を取ると、次のような形になります。
$$\begin{eqnarray}
\log { \rm Gam } (x |a,b) = (a-1)\log x -bx +const
\end{eqnarray}$$
\(\sigma ^2 \)にも事前分布を仮定するので、同時分布は次のようになります。
$$\begin{eqnarray}
p(Y,X,W,\mu, \sigma^{-2} ) =p(W) p(\mu ) p(\sigma^{-2} )\prod_{n} p(y_n | x_n , W, \mu , \sigma ^{-2} ) p(x_n )
\end{eqnarray}$$
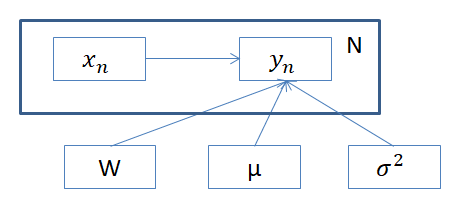
計算するべき事後分布も、以下のように近似しましょう。
$$\begin{eqnarray}
p(X,W,\mu , \sigma ^{-2} | Y ) \sim q(X)q(W) q(\mu )q(\sigma ^{-2} )
\end{eqnarray}$$
近似分布のパラメーターは、\(q(\sigma ^{-2} \)以外は、上で計算した計算結果とほぼ同じです。\( \sigma ^{-2} \)を期待値\( E[\sigma ^{-2} ] \)に置き換えるだけです。
\(\sigma ^{-2} \)が出現するのは、 \(p(\sigma ^{-2} ) \)と、\( p(y_n | x_n , W, \mu , \sigma ^{-2} ) \)のexp の中と、正規分布の規格化定数\( \sqrt{\sigma ^{-2} } \)の部分です。
それを考慮すると、\(q (\sigma ^{-2} ) \)は以下のようになります。
$$\begin{eqnarray}
q( \sigma ^{-2} ) &=& {\rm Gam } (\sigma ^{-2} |\hat{a} , \hat{b} ) \\
\hat{a} &=&a+N/2 \\
\hat{b} &=& b-\frac{1}{2} \sum_{n} \left[ E[x_n ^T ] E[WW^T ] E[x_n] -2(y_n -E[\mu ] ) ^T E[W]E[x_n ] +|y_n – E[\mu] |^2 \right]
\end{eqnarray}$$
また、期待値は、
$$\begin{eqnarray}
E[\sigma ^{-2} ] = \frac{\hat{a}}{\hat{b}}
\end{eqnarray}$$
で与えられます。
まとめ
- PPCAの解説を簡単にした
- 平均場近似の解説を簡単にした
- ベイズ主成分分析の簡単なバージョンを計算した
- ベイズ主成分分析を少しだけ難しくしたバージョンを計算した

