変分推論によるポアソン混合モデルの近似を、pythonで実装して遊んでみる記事です。
詳しい計算は、変分推論の記事を読んでみてください。

記事で使っているソースコードはgithub に置いてあります。
https://github.com/msamunetogetoge
元ネタは、PRMLの10章 と緑本の4章です。
変分推論
初めに、使うモデルや、更新式をメモしておきます。モデルはポアソン混合モデルで、以下の式で定義されます。
$$\begin{eqnarray}
p(X, S , \lambda , \pi ) &=& p(X|S, \lambda )p(S|\pi)p(\pi ) p(\lambda ) \\
p(X| S , \lambda ) &=& \prod_{n} p(x_n | s_n , \lambda ) \\
p(x_n | s_n , \lambda ) &=& \prod_{k} {\rm Poi} (x_n |\lambda _k ) ^{s_{n,k} } \\
p(S |\pi ) &=& \prod p(s_n|\pi) \\
p(s_n|\pi) &=& {\rm Cat}(s_n , \pi ) = \prod \pi_k ^{s_{n,k}} \\
p(\lambda _k ) &=&{ \rm Gam } (\lambda _k | a,b ) \\
&=& C_{G}(a, b ) \lambda ^{a-1} \exp(-b\lambda _k )\\
p(\pi )= &=& { \rm Dir} (\pi |\alpha ) \\
&=&C_{D}(\alpha ) \prod \pi _{k} ^{\alpha _k -1}
\end{eqnarray}$$
1
このモデルは、\(S , \lambda \)を与える事で、データ\(x \)をサンプリングすることが出来ます。
\(S , \lambda \)も確率分布からサンプリングする必要がありますが、それには、\(a, b, \alpha \)を決定しなくてはなりません。
\( a, b, \alpha \)を決めるための更新式は以下の式になります。
$$\begin{eqnarray}
q^{\ast}(s_n ) &=& {\rm Cat }(s_n|\eta _n )\\
\eta _{n,k} &\propto & x_n E_{\lambda _k }[ \log \lambda _{k} ]- E_{\lambda _k }[ \lambda _k ]
+ E_{\pi _k } [\log \pi _k] \\
q^{\ast} (\lambda _k ) &=& { \rm Gam } (\lambda _k|\hat{a}_k , \hat{b}_k )\\
\hat{a}_k &=& \sum _{n} E_S [s_{n,k} ]x_n +a \\
\hat{b}_k &=& \sum_{n} E_S [s_{n,k} ] + b \\
q^{\ast} (\pi ) &=& {\rm Dir } (\pi |\hat{\alpha } )\\
\hat{\alpha _k } &=& \sum_{n} E_{S} [s_{n,k} ] +\alpha _{k}
\end{eqnarray}$$
期待値は以下の式から計算出来ます。
$$ \begin{eqnarray}
E_{\lambda _k }[ \lambda _{k} ] &=& \hat{a} /\hat{b}\\
E_{\lambda _k }[ \log \lambda _{k} ] &=& \psi (\hat{a} ) – \log \hat{b} \\
E_{\pi _k }[ \log \pi _{k} ] &=& \psi (\hat{\alpha _k }) -\psi (\sum \hat{ \alpha _k })\\
E_S[ s_{n,k} ] &=& \eta _{n,k}
\end{eqnarray}$$
事前分布と、パラメーター更新後の分布が一致しているので、パラメーターを更新する数を決めて計算することで、与えられたデータの、ポアソン混合モデルによる近似が得られます。
変分推論のpython による実装
適当なデータを生成しておいて、上記の変分推論でフィッティングしてみます。
x1 = np.random.poisson(lam=3, size=700)
x2= np.random.poisson(lam=15, size=300)
x=np.append(x1,x2)変分推論を行うクラスをpythonで実装します。パラメーターの意味は、上でした計算と同じです。
class VI():
def __init__(self,K,x,a,b,alpha):
self.K =K
self.x=x
self.a = a
self.b =b
self.alpha =alpha
def Estep(self): #期待値の計算
self.E_lam = self.a/self.b
self.E_loglam = psi(self.a) -np.log(self.b)
self.E_logpi =psi(self.alpha) - psi(np.sum(self.alpha))
log_eta = np.dot(self.x.reshape(len(self.x), 1), self.E_loglam.reshape(1,self.K)) -self.E_lam + self.E_logpi
log_eta =log_eta.T- np.max(log_eta, axis=1)
self.E_s = (np.exp(log_eta)/np.sum(np.exp(log_eta),axis=0 )).T
return self.E_s
def Mstep( self): #パラメーターを更新
self.E_s =self.Estep()
a_hat =np.dot(self.x, self.E_s ) + self.a
b_hat = np.sum(self.E_s, axis=0) +self.b
alpha_hat = np.sum(self.E_s,axis=0)+self.alpha
return a_hat , b_hat, alpha_hat
def itr_calc(self,max_itr ): #計算を繰り返す関数
A=np.zeros((self.K,max_itr))
B=np.zeros((self.K,max_itr))
for i in range(max_itr):
self.a,self.b,self.alpha = self.Mstep()
A[:,i]=self.a
B[:,i]=self.b
Lam = A/B
lam = self.a / self.b
self.E_pi = self.alpha/np.sum
return lam, Lam一応クラスの中身の説明をします。
Estep でパラメーターを更新するのに必要な期待値を計算しています。
Mstepでパラメーターを更新しています。
itr_calc で指定した回数だけ計算し、\( \lambda \)を返しています。この時に、\( \pi \)の値が分かっていれば、その割合でポアソン分布を生成すればよいので、クラスで値を保持しています。
計算させてみましょう。
K=2
a=np.abs(np.random.randn(K))
b=5*np.abs(np.random.randn(K))
alpha = np.abs(np.random.randn(K))
cal = VI(K=K, x=x, a=a, b=b, alpha=alpha)
lam,Lam, E = cal.itr_calc( max_itr= 1000)
print(lam)
print(cal.E_pi)
#[ 2.90780907 14.82726769]
#[0.69099361 0.30900639]データは\(\lambda =3, 15 \)のポアソン分布を\( 7:3 \)の割合で生成していました。結構いい感じにフィッティング出来ています。重ねてヒストグラムにしてみましょう。
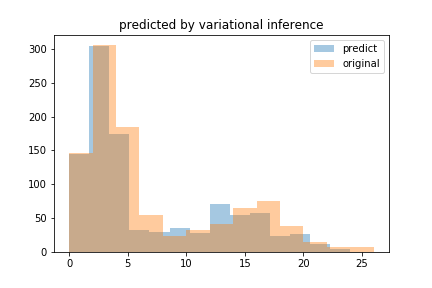
\( \lambda \)がどのように推移しているかを見てみます。
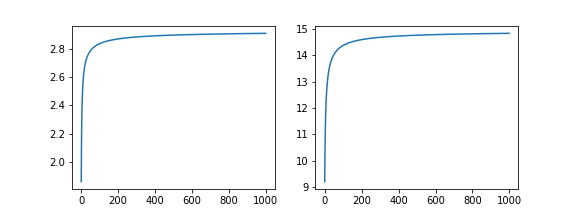
グラフを見ると、500回計算したころには、収束しているような気がします。パラメーターの更新を、計算回数で制御するのでなくて、ELBOで制御する方法があります。
EM-like 変分推論
ELBO \( \mathcal{L}(q, \theta) \)は以下の式で定義されます。
$$\begin{eqnarray}
\log p(X| \theta ) &=& \mathcal{L}(q, \theta) +KL(q \| p) \\
\mathcal{L}(q, \theta) &=& E_{Z}\left[ \log \left\{ \frac{p(X,Z| \theta )}{q(Z)} \right\} \right]
\end{eqnarray} $$
ポアソン混合モデルの、場合は以下のように計算出来ます。
$$\begin{eqnarray}
\mathcal{L}(q, \theta) &=& \sum_n
\left\{ E_{\lambda} [ E_{s_n} [ \log p(x_n |s_n , \lambda ) ]]+
E_{s_n} [E_{\pi}[ \log p(s_n | \pi ) ]] – E_{s_n} [\log q_{ {\rm new } }(s_n )] \right\} \\
&-& KL[ q_{ {\rm new } }( \lambda ) ][ q_{ {\rm old } }( \lambda )] – KL[ q_{ {\rm new } }( \pi ) ][ q_{ {\rm old } }( \pi )]
\end{eqnarray} $$
期待値を計算します。
$$\begin{eqnarray}
E_{\lambda} [ E_{s_n} [ \log p(x_n |s_n , \lambda ) ]] &=& \sum_k \left( E_{s_n} [s_{n,k} ] ( x_n E_{\lambda _k }[ \log \lambda _{k} ]- E_{\lambda _k }[ \lambda _k ] ) \right) \\
E_{s_n} [E_{\pi}[ \log p(s_n | \pi ) ]] &=& \sum_k \left( E_{s_n} [s_{n,k} ] E_{\pi}[\log \pi _k ] \right)\\
E_{s_n} [\log q_{ {\rm new } }(s_n )] &=&\sum_k E_{s_n} [s_{n,k} ] \pi_{k} \\
KL[ q_{ {\rm new } }( \lambda ) ][ q_{ {\rm old } }( \lambda )] &=&
\sum_k \left( ( {a_{\rm new }}_k – {a_{\rm old }}_k )E_{\lambda _k } [\log \lambda _k ] –
({b_{\rm new }}_k – {b_{\rm old }}_k ) E_{\lambda _k } [ \lambda _k ] \right) \\
KL[ q_{ {\rm new } }( \pi ) ][ q_{ {\rm old } }( \pi )] &=&
\sum_k \left( {\alpha_{\rm new }}_k – {\alpha_{\rm old }}_k \right) E_{\pi _k} [\pi _k]
\end{eqnarray}$$
python でELBOを計算する関数を定義して、計算させてみましょう。
class EM_like_VI(VI):
def Elbo(self):
a_hat , b_hat, alpha_hat = self.Mstep()
pi = np.random.dirichlet(self.alpha , size=1)
self.E_pi = pi/np.sum(pi)
E_1 = np.dot(self.x.reshape(len(self.x), 1), self.E_loglam.reshape(1,self.K)) -self.E_lam
E_1 = np.sum(np.sum(E_1*self.E_s, axis=1))
E_2 = np.sum(np.dot(self.E_s, self.E_logpi))
E_3 = np.sum(np.dot(self.E_s, pi.T ))
E_4 = np.sum((a_hat - self.a)*self.E_loglam - (b_hat - self.b)*self.E_lam )
E_5 = np.sum( (alpha_hat - self.alpha)*self.E_pi)
self.elbo = E_1+E_2 -E_3 -E_4 - E_5
return self.elbo
def itr_elbo(self,max_itr ):
E=[]
A=np.zeros((self.K,max_itr))
B=np.zeros((self.K,max_itr))
for i in range(max_itr):
elbo=self.Elbo()
self.a,self.b,self.alpha = self.Mstep()
self.elbo= self.Elbo()
E=np.append(E,self.elbo)
A[:,i]=self.a
B[:,i]=self.b
if np.abs(self.elbo - elbo )<0.01 :
print("Convergence !! n={}".format(i+1))
break
Lam = A/B
lam = self.a / self.b
return lam, Lam, E前に定義したクラスVI を継承して、Estep, Mstepをリサイクルしています。
itr_elbo を呼び出すと、更新後にELBOの差が0.01 になるまで計算を繰り返し、selg.Eに計算値が格納されます。遊ぶときは、max_itr とELBOの差を変数にした方が良いかもしれません。2
前に生成したデータをフィッティングして、グラフを描いてみます。
lam,Lam, E = cal.itr_elbo( max_itr= 1000)
#Convergence !! n=91
print(lam)
print(cal.E_pi)
#[15.1801266 2.94556311]
#[[0.30006211 0.69993789]]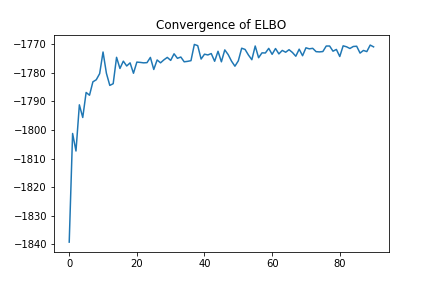
ELBOを監視することにより、計算回数を大幅に減らすことが出来ました。3
github のjupyter notebook には、混合ポアソンモデルでは上手くフィッティング出来ないデータも載せているので、よかったら見てください。
まとめ
- 混合ポアソンモデルの変分推論をpythonで実装した。
- 混合ポアソンモデルの場合に、elboを計算した。
- elboを計算するクラスをpythonで実装した。



