PPCAで画像を圧縮してみる | マサムネの部屋

先日、最尤推定でPPCAを行う記事を書きました。その結果を用いて、mnist のデータの次元を圧縮してみます。

PPCA
画像の生成
まとめ

PPCA

詳しい計算は解説の記事を見てもらうとして、問題設定と答えを書いておきます。

D次元のデータ$x $がN個あるとき、データをM次元に圧縮したい。
一つの方法として、データがM次元正規分布に従う隠れ変数$z $によって生成されていると考える。
$$\begin{eqnarray}
z &\sim & \mathcal{N}(0,I )\\
x&=&Wz+\mu + \epsilon \\
\epsilon &\sim & \mathcal{N} (0,\sigma ^2 I ) \\
p(x|z ) &=& \mathcal{N} (x| Wz + \mu , \sigma ^2 )
\end{eqnarray}$$
この状況で、zをサンプルしてデータを取り直す事で、$D$次元のデータが$ M $次元のデータで代替できる。
ベイズの定理から、$ p(z|x ) $は
$$\begin{eqnarray}
K&=& W^T W +\sigma ^2 I_{M} \\
p(z|x ) &=& \mathcal{N}(z |K^{-1} W^T (x-\mu ) , \sigma^{-2} K^{-1} )
\end{eqnarray}$$
と表す事が出来る。データが全部でNこある時、最尤推定でパラメーター$\mu, W, \sigma ^2 $で求めると次のようになる。

$$\begin{eqnarray}
\hat{ \mu } &=& \frac{x_n}{N} \\
\hat{W} &=& U(K- \sigma ^2 I_{D} )V^T \\
\hat{\sigma ^2} &=& \frac{1}{D-M} \sum_{j=M+1} ^{D}s_j
\end{eqnarray}$$
ただし、U,K,Vは
$$\begin{eqnarray}
{\rm diag} K&=&
\begin{cases}
s_j & j\leq M \\
\sigma ^2 & j>M
\end{cases} \\
U &=&(u_1 , \cdots , u_D ) \\
S&=& X^.T X
Su_j &=& s_j u_j \\
V^T V &=&I \\
V V^T &=& I
\end{eqnarray}$$
を満たすもの。

計算の手順としては、

Sの特異値を求める
Mを決める
最尤推定量の計算をする

という感じです。

画像の生成

colab 上で、MNISTデータ¹に対してPPCAを行ってみます。Mの値を適当に変えて、どんな画像が生成されるのか確かめます。²

import numpy as np
import matplotlib.pyplot as plt

from keras.datasets import mnist 
(x_train, y_train), (x_test, y_test) = mnist.load_data()
#データを全部使うと計算に時間がかかるので1000個だけ使う
X = x_train.reshape(x_train.shape[0],-1)[:1000,:]

S= np.dot(X.T,X)
#s_jたちとUを求める
V,s,U = np.linalg.svd(S,full_matrices=False)

#sのバープロットを見る。これで大きい特異値と小さい特異値の差が大きければ次元の削減が上手くいく
plt.bar(range(len(s)),s/np.sum(s))
plt.ylim(0,0.03)
plt.title("singular value of mnist")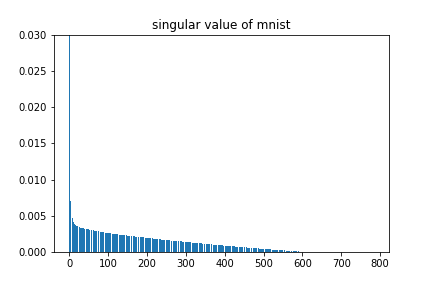

データが28×28=784次元ですが、大きな値を持つ特異値があまりないので、微妙な気配です。適当な次元を設定し、最尤推定量を計算して0を表した画像を生成してみます。

#計算に使う次元
Ms = [10,50,100,400,700]

plt.figure(figsize=(12,5))
for i,M in enumerate(Ms):
    #最尤推定
    sig = (1/(len(s)-M)) * np.sum(s[M+1:])
    k=s
    k[M+1:]=sig
    W=np.random.randn(len(s)*M).reshape(len(s),M)
    V_W,s_W,U_W = np.linalg.svd(W, full_matrices=False)
    K=np.diag(k)
    W_ml = np.dot(np.dot(U,K-sig),V_W)
    #データ生成
    x=X[1]
    K=np.dot(W_ml.T , W_ml)+sig
    K_inv = np.linalg.inv(K)
    mu_z = np.dot(np.dot(K_inv ,W_ml.T) ,(x-mu[0]))
    Sig_z =K_inv/sig
    #zのサンプリング
    z=mu_z

    mu_x = np.dot(W_ml , z.reshape(-1,1))+mu[0]
    Sig_x = sig*np.eye(len(x))
    #xのサンプリング
    sample_x=mu_x
    #どんなデータが出来たか見る
    plt.subplot(1,len(Ms),i+1)
    plt.title(f"dim={M}")
    plt.imshow(sample_x.reshape(28,28))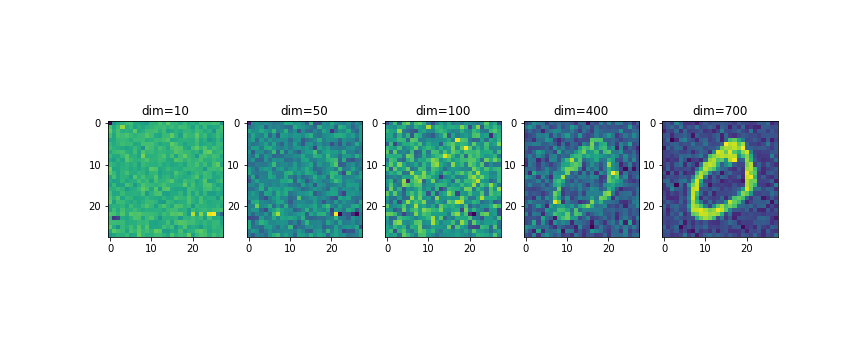

M=50くらいからほんのり輪郭が出始め、dim=400くらいで元の画像が判別できるようになっています。元々の次元が784なので、大体半分くらいの大きさのデータで再現出来ている事になります。
今回のように、形が判別できれば良いだけなのか、もっと詳細な情報が欲しいのかによって、必要なMの大きさが変わってくるので注意が必要そうです。