PTBコーパスを使って、 言語モデルを作ります。つまり、単語の列を与えたときに、次に来る単語を予測するモデルを作ります。その為に必要な関数を実装して、モデルの学習を行います。また、このモデルが意味のあるものになっているか、コサイン類似度を用いて評価してみます。
前回の記事はこちら。

Embedding 層
パソコンに言葉を理解させるには、単語をベクトルや行列で表す必要があります。単語をベクトルで表現することを分散表現と呼びます。単語をベクトルで表すと、単語の意味の近さを測れたり、単語同士の足し算が出来たりと、便利な事があります。
分散表現を得る事に相当する層は、Embedding 層と呼ばれます。ニューラルネットワークでいう所の中間層ですが、入力から中間層への行列\( W \)が、分散表現になります。
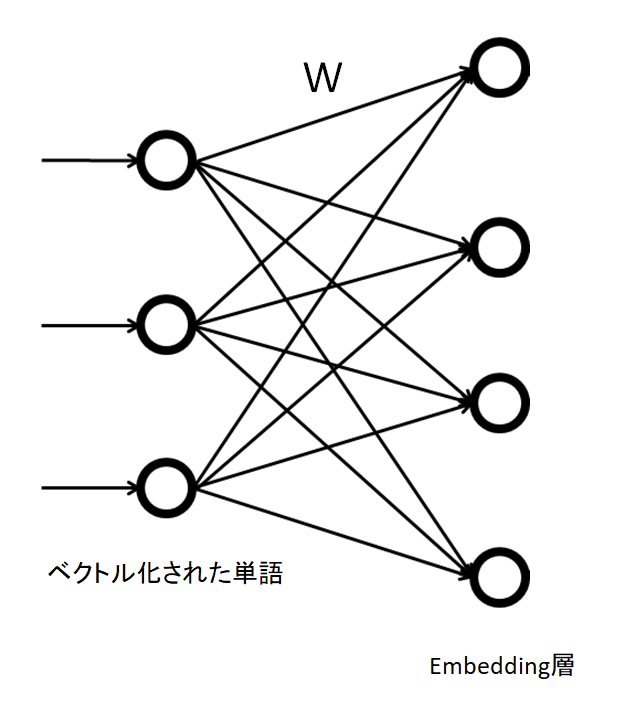
単語がone hot encoding されている時は、単語に相当する番号の行を抜き出すだけの操作になります。そのようになっていると仮定して、実装します。 python で実装すると以下のようになります。
class Embedding:
def __init__(self, W):
self.params = [W]
self.grads = [np.zeros_like(W)]
self.idx = None
def forward(self, idx):
W, = self.params
self.idx = idx
out = W[idx]
return out
def backward(self, dout):
dW, = self.grads
dW[...] = 0
np.add.at(dW, self.idx, dout)
return Noneモデルの概略図と関数の実装
作るモデルの概略を書いておきます。

単語のベクトルが入ってきたら分散表現に変換し、RNNと全結合層で学習します。損失関数はsoftmaxにします。RNNは簡単に勾配消失が起きてしまうので、例えば10個とかで、誤差逆伝搬を断ち切りたい1のでした。
Embedding, Affine, softmax関数を、 TimeEmbedding, TimeAffine, TimeSoftmaxWithLossという名前で、 実装します。RNNについては、前回TimeRNNという形で実装しました。softmax関数は、ベクトルに\(x\) に対して以下を対応させる関数です。
$$\begin{eqnarray}
{\rm softmax } (x) = \frac{\exp (x)}{\sum_{i} \exp (x_i)}
\end{eqnarray}$$
TimeEmbeddingについては、Embedding 層をT個用意して、それぞれ計算するだけです。
TimeAffine も同様ですが、2次元の行列を作って一度に計算してから3次元にバラします。
TimeSoftmaxWithLoss は、 損失関数を\(t \)方向に平均を取って一つの値とします。 ラベルが-1となっている部分は無視するようにしておきます。
softmax関数は定義せずに使っていますが、以下の記事で定義しています。

import numpy as np
#softmax 関数は定義して無いですが、昔の記事にあるので使ってください。
class TimeAffine: #全結合の変形
def __init__(self, W, b):
self.params = [W, b]
self.grads = [np.zeros_like(W), np.zeros_like(b)]
self.x = None
def forward(self, x):
N, T, D =x.shape
W, b = self.params
rx =x.reshape(N*T, -1)
out = np.dot(rx, W)+b
self.x = x
return out.reshape(N,T,-1)
def backward(self, dout):
x =self.x
N, T, D = x.shape
W, b = self.params
dout = dout.reshape(N*T, -1)
rx =x.reshape(N*T, -1)
db = np.sum(dout, axis=0)
dW = np.dot(rx.T, dout)
dx = np.dot(dout, W.T)
dx = dx.reshape(*x.shape)
self.grads[0][...] = dW
self.grads[1][...] = db
return dx
class TimeEmbedding: #Embedding層の変形
def __init__(self, W):
self.params = [W]
self.grads = [np.zeros_like(W)]
self.layers = None
self.W = W
def forward(self, xs):
N, T = xs.shape
V, D = self.W.shape
out = np.empty((N, T, D), dtype='f')
self.layers = []
for t in range(T):
layer = Embedding(self.W)
out[:, t, :] = layer.forward(xs[:, t])
self.layers.append(layer)
return out
def backward(self, dout):
N, T, D = dout.shape
grad = 0
for t in range(T):
layer = self.layers[t]
layer.backward(dout[:, t, :])
grad += layer.grads[0]
self.grads[0][...] = grad
return None
class TimeSoftmaxWithLoss: #損失関数の計算の変形
def __init__(self):
self.params, self.grads =[], []
self.cache = None
self.ignore_label = -1
def forward(self, xs, ts):
N, T, V = xs.shape
if ts.ndim ==3: #ラベルがone hot encodingされている時用
ts = ts.argmax(axis=2)
mask = (ts!= self.ignore_label) #-1が付けられたラベルは無視するようの目印
xs = xs.reshape(N*T, V)
ts = ts.reshape(N*T)
mask = mask.reshape(N*T)
ys = softmax(xs)
ls = np.log(ys[np.arange(N * T), ts])
ls*= mask
loss = -np.sum(ls)
loss/= mask.sum()
self.cache = (ts, ys, mask, (N, T, V))
return loss
def backward(self, dout=1):
ts, ys, mask, (N, T, V) =self.cache
dx = ys
dx[np.arange(N*T), ts]-=1
dx*= dout
dx/= mask.sum()
dx*= mask[:, np.newaxis]
dx = dx.reshape((N,T,V))
return dxsoftmax関数に適当な数字とラベルを放り込んでみます。
xs = np.ones((100,20,2))
ts = np.random.binomial(1, 0.5, 2000).reshape(100,20)
timesoft = TimeSoftmaxWithLoss()
timesoft.forward(xs, ts)
#0.6931471805599454動いたのでよしとしましょう。次に、初めに貼った図のようにモデルを作ります。
モデルの作成
モデルを作ります。クラスで必要な層は揃えているので、次元に気を付けて組み立てるだけです。SimpleRnnlmという名前のクラスで実装します。embed_W というパラメーターがptbコーパスの分散表現になります。
forward で損失関数を計算し、 backward で微分を計算します。
class SimpleRnnlm:
def __init__(self, vocab_size, wordvec_size, hidden_size):
V, D, H =vocab_size, wordvec_size, hidden_size
rn = np.random.randn
#重み
embed_W =(rn(V, D) / 100).astype("f")
rnn_Wx =(rn(D, H)/ np.sqrt(D)).astype("f")
rnn_Wh = (rn(H,H) / np.sqrt(H)).astype("f")
rnn_b = np.zeros(H).astype('f')
affine_W = (rn(H, V) / np.sqrt(H)).astype("f")
affine_b = np.zeros(V).astype("f")
#層を並べておく
self.layers = [
TimeEmbedding(embed_W),
TimeRNN(rnn_Wx, rnn_Wh, rnn_b),
TimeAffine(affine_W, affine_b)
]
self.loss_layer = TimeSoftmaxWithLoss()
self.rnn_layer = self.layers[1]
#重みと勾配のリスト作成
self.params, self.grads = [], []
for layer in self.layers:
self.params+= layer.params
self.grads+= layer.grads
def forward(self, xs, ts):
for layer in self.layers:
xs = layer.forward(xs)
loss = self.loss_layer.forward(xs, ts)
return loss
def backward(self, dout = 1):
dout =self.loss_layer.backward(dout)
for layer in reversed(self.layers):
dout = layer.backward(dout)
return doutモデルの学習
ニューラルネットワークのように、損失関数を頼りに、モデルを訓練します。実装が一番簡単な、SGD(確率的勾配降下法)でパラメーターを更新します。また、初期値としてXavier の初期値を使います。SGDと相性が良いとされる初期値2です。
今回は、コーパスから最初の1000個までの単語を対象に学習を行います。また、分散表現は何次元のベクトルで作るか、という問題がありますが、本に載っていた数字\(D = 100\) をそのまま使います。全結合層も特に意味はなく、\(H=100\) 次元にしています。時間のサイズは\( T=5\) 3 です。
学習に必要なコード 4 と、実行結果のグラフを描きます。
from dataset import ptb
class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for i in range(len(params)):
params[i] -= self.lr * grads[i]
# ハイパーパラメータの設定
batch_size = 10
wordvec_size = 100
hidden_size = 100
time_size = 5 # Truncated BPTTの時間サイズ
lr = 0.1
max_epoch = 300
# 学習データの読み込み
corpus, word_to_id, id_to_word = ptb.load_data('train')
corpus_size = 1000
corpus = corpus[:corpus_size]
vocab_size = int(max(corpus) + 1) #412単語あります。
xs = corpus[:-1] # 入力
ts = corpus[1:] # 出力
data_size = len(xs)
max_iters = data_size//(batch_size* time_size)
time_idx = 0
total_loss = 0
loss_count = 0
loss_list =[]
# モデルの生成
model = SimpleRnnlm(vocab_size, wordvec_size, hidden_size)
optimizer = SGD(lr)
# ミニバッチの各サンプルの読み込み開始位置を計算
jump = (corpus_size - 1) // batch_size
offsets = [i*jump for i in range(batch_size)]
#学習
for epoch in range(max_epoch):
for iter in range(max_iters):
batch_x = np.empty((batch_size, time_size), dtype = "i")
batch_t = np.empty((batch_size, time_size), dtype = "i")
for t in range(time_size):
for i, offset in enumerate(offsets):
batch_x[i,t] = xs[(offset + time_idx) % data_size]
batch_t[i,t] = ts[(offset + time_idx) % data_size]
time_idx += 1
loss = model.forward(batch_x, batch_t)
model.backward()
optimizer.update(model.params, model.grads)
total_loss += loss
loss_count += 1
total_loss = total_loss/loss_count
print("Loss = {}".format(total_loss))
loss_list.append(total_loss)
total_loss, loss_count = 0, 0 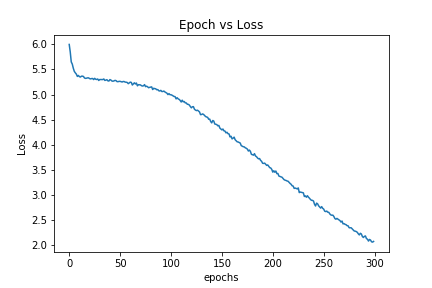
一度学習が止まっていますが、何回か繰り返す間にデータを学習していることが分かります。412個の単語を100次元のベクトルで表し、文を入力すればその次に来る単語を予測するモデルが出来ました。
勿論このモデルでは、学習に使った単語以外が載っている文は扱えませんし、単語をベクトルにすることも出来ません。
とは言え、412単語の中でなら好きに遊べるので、このモデルで遊んでみましょう。1000エポック回しましたが、lossの値が0.6くらいで止まってしまったので精度は期待できません。
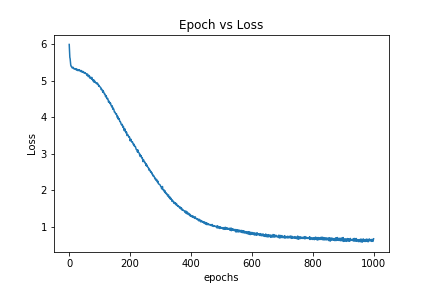
単語同士の近さを測る
ベクトル同士が似ているかどうか測りたい時は、内積を取ってそれぞれのベクトルの絶対値で割ってみると良いです。0に近ければ似ていなくて、±1に近ければ似ています。5この類似度を、この記事内ではコサイン類似度と呼び、単語a, b のコサイン類似度を\( \cos ({\rm a, b} ) \)で表します。
$$\begin{eqnarray}
\cos({\rm a,b} )= \frac{ a\cdot b}{\|a \| \|b \| }
\end{eqnarray}$$
意味が似てるような単語でコサイン類似度を計算させてみます。
$$\begin{eqnarray}
\cos({\rm join , group} )&=& 0.04 \\
\cos({\rm old , once} )&=& 0.36 \\
\cos({\rm researchers , university} )&=& 0.23 \\
\cos({\rm but , although } )&=& 0.16
\end{eqnarray}$$
とても人様にお見せできるような結果ではありません。お遊びのシンプルなモデルならこんなもんです。
次回はLSTMを実装し、大きなコーパスで計算してみます。
まとめ
- モデル構築のための関数を定義した。
- 単純なモデルを作成した
- モデルを訓練した。
- シンプルなRNNだとパソコンに言葉を理解させることは叶わなかった。
- Truncated BPTT と呼んでいました。
- アルゴリズムと初期値の関係は別の記事でまとめたいと思っています。
- 微分の情報が単語5つ分しか伝わらないので、言葉の意味をモデルが理解するのは難しいかもしれません。
- ptbコーパスは、 https://github.com/oreilly-japan/deep-learning-from-scratch-2 のdataset からimport して使用しています。
- 統計で出てくる相関係数とか、コサインの事です。

