絶対に理解できる統計的仮説検定

多くの人が一度は躓く仮説検定について解説します。
そんなに難しい話ではないので、ゆっくり読んでみてください。

何故仮説検定を行うのか？
帰無仮説と対立仮説
有意水準
統計的仮説検定
統計的仮説検定の例
まとめ

何故仮説検定を行うのか？

まずはモチベーションが大事なので、何故仮説検定を使うのかを書きます。
良くある状況として、何かパラメーターをコントロールして、数種類のデータを得たとします。¹があるとき、それらは全て同じデータでしょうか？
仮に違うとして、何が違うのでしょうか。
統計的仮説検定はそのような問いに答える事が出来ます。²しかも、下した結論がどのような仮定に基づき、どの程度間違いの確率を含んでいるかを明確にすることが出来ます。
何か施策を講じたとき、効果や次の一手を考えるための材料になります。³
モチベーションを高めたところで、詳しい説明に入ります。

帰無仮説と対立仮説

統計的仮説検定は、基本的には背理法です。
帰無仮説と、その否定である対立仮説を用意する事から始めます。
そして、帰無仮説を否定して、対立仮説が正しいと言いたいのが統計的仮説検定です。
従って、対立仮説に、示したいことを持ってくるのが普通のやり方になります。
例えば、何か施策を講じて、商品の売り上げアップを目指したとします。施策前後を比べると、売り上げが変わってるはずなので、ある期を境にして売り上げデータを2種類に分割すれば、平均値が変わっているはずです。このような時は、帰無仮説と対立仮説を以下のように設定します。
$$\begin{eqnarray}
帰無仮説 H_0 &:& \mu= \mu _1 – \mu _2=0 \\
対立仮説H_1 &:& \mu \neq 0
\end{eqnarray}$$
ただし、$ \mu _i $で平均値を表しています。もちろん、$ \mu _! \geq \mu _2 $を対立仮説にすることも出来ます。⁴
帰無仮説と対立仮説の設定について、一般的に述べておきます。
$ \theta $について検定を行いたいとします。
$ \Theta $で、$ \theta $が取り得る値全てを表します。また、$ \Theta _0 $を帰無仮説が表す$ \theta $の値全てとします。
こうすると、帰無仮説と対立仮説は以下のように書けます。
$$\begin{eqnarray}
帰無仮説 H_0 :\theta \in \Theta _0 \\
対立仮説H_1 : \theta \in \Theta _0 ^c
\end{eqnarray}$$
ただし、集合$A \subset X $に対して、$A^c $でXでの補集合を表しています。
帰無仮説と対立仮説を設定するのは、$ \theta $が、$ \Theta _0 , \Theta _0 ^c $どちらに属するのか？という問題を建てる事と同義です。
例えば、2種類のデータの平均値が等しいか調べる例では、
$$\begin{eqnarray}
\mu \in \Theta &=& ( -\infty , +\infty ) \\
\Theta _0 &=& \{ 0\} \\
\Theta _0 ^c &=& ( -\infty , 0) \cup ( 0, +\infty )
\end{eqnarray}$$
となります。⁵

有意水準

ところで、帰無仮説はどうやって否定するのでしょうか。
2種類のデータの平均値を比べる問題に戻ってみます。
言いたいことは$ \mu _1 \neq \mu _2 $なので、適当な数字Cを使って、
$$\begin{eqnarray}
|\mu| =| \mu _1 – \mu _2 | > C
\end{eqnarray}$$
なら、帰無仮説を否定する、という戦略が考えられます。⁶
つまり、
$$\begin{eqnarray}
\mu \in \Theta _c = \{ \mu | | \mu |>C \}
\end{eqnarray}$$
の時、帰無仮説を否定するのです。$ \Theta _c $を棄却域と呼んだりします。
Cを決めるには、どうしたら良いでしょうか？
ここで登場するのが有意水準$ \alpha $と確率です。⁷
有意水準とは、帰無仮説$ H_0 $が正しいのに、誤って否定してしまう確率の上限の事で、式で書くと次のようになります。
$$\begin{eqnarray}
\sup _{\theta \in \Theta _0 } P_{\theta}( H_0 を否定) \leq \alpha \Leftrightarrow
\sup _{\theta \in \Theta _0 } P_{\theta}( \theta \in \Theta _{c} ) \leq \alpha
\end{eqnarray}$$

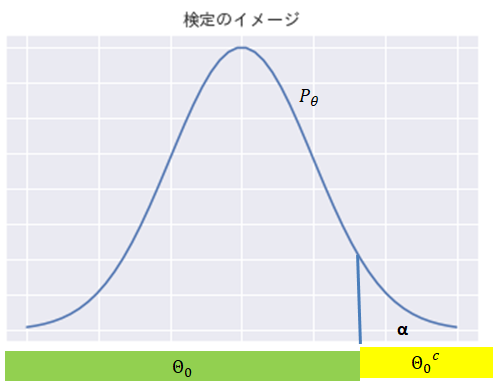
$ \alpha $と、$ \theta $が従う確率分布を指定すれば、 $ \Theta _c $が決まるので、
$$\begin{eqnarray}
\theta \in \Theta _c
\end{eqnarray}$$
の時に帰無仮説を否定するとすれば、客観的な指標が得られ、この決定が間違っている確率は$ \alpha $という事になります。
2種類のデータの平均値を比べる問題で具体的に$C $を決定してみます。

2種類のデータの差が、正規分布$ \mathcal{N}( \mu , \sigma ^2 ) $に従うとして、データを$X_1 , \cdots , X_n $のn 個取得したとします。⁸⁹

[$ \Theta _c $を決める計算の例]
$ \Theta _0 $が一点なので、$ \Theta _c $を決定する式は以下のように書けます。
$$\begin{eqnarray}
P_{ \mu =0} ( |\bar{X} | >C) \leq \alpha
\end{eqnarray}$$
ただし、$ \bar{X} =\sum X_i /n $です。
今、$ \bar{X} $は、正規分布$ \mathcal{N} (\mu, \sigma^2 /n )$に従うので、$ \mu = 0 $の仮定の元で
$$\begin{eqnarray}
Z= \sqrt{n} \bar{X} /\sigma \sim \mathcal{N} (0,1)
\end{eqnarray}$$
となります。従って、確率の部分を
$$\begin{eqnarray}
P_{ \mu =0} ( |\bar{X} | >C) &=& P( | Z | >\sqrt{n}C / \sigma ) \\
&=& 2*P( Z>\sqrt{n}C / \sigma )
\end{eqnarray}$$
と書き換える事が出来ます。具体的に表示すると、
$$\begin{eqnarray}
P_{ \mu =0} ( |\bar{X} | >C)= 1-2*\int_{0 )} ^{\sqrt{n}C / \sigma )}
\frac{1}{\sqrt{2 \pi }}\exp(- \frac{z^2}{2})
\end{eqnarray}$$
となります。これの値が$ \alpha $となるようにC を定めれば良いです。
つまり、
$$\begin{eqnarray}
1-2*\int_{0 } ^{\sqrt{n}C / \sigma }
\frac{1}{\sqrt{2 \pi }}\exp(- \frac{z^2}{2}) dz =\alpha
\end{eqnarray}$$
の式の、積分の上限を$z_{\alpha /2 } $と置いて、
$$\begin{eqnarray}
C= (\sigma /\sqrt{n})z_{\alpha /2 }
\end{eqnarray}$$
と定めるのです。同じことですが、
$$\begin{eqnarray}
P(Z>z_{\alpha /2 }) =\alpha /2
\end{eqnarray}$$
の式を満たすように$ z_{\alpha } $を定めて、 $ C= (\sigma /\sqrt{n})z_{\alpha /2 }$でも良いです。
このCを用いて、棄却域は、
$$\begin{eqnarray}
\Theta _c = ( -\infty , -|C| ) \cup (|C| , \infty )
\end{eqnarray}$$
と表す事が出来ます。¹⁰

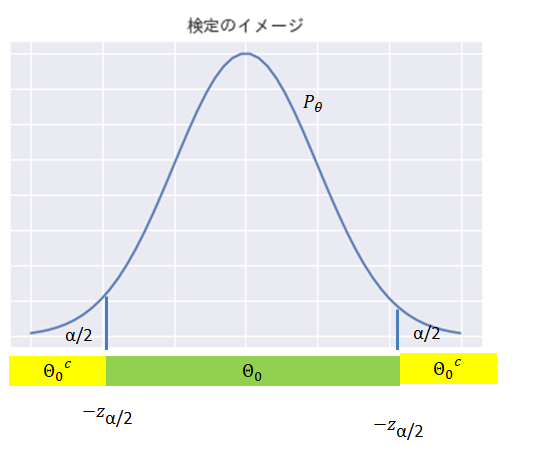
$ \mu >0 $を言いたい場合も、同じような計算を行う事で棄却域を特定できます。
検定を行う為に帰無仮説と対立仮説を用意する事、帰無仮説を否定するために、有意水準と確率分布を用意する必要がある事を見てきました。

統計的仮説検定

統計的仮説検定の手法についてまとめておきます。統計的仮説検定は、以下の手順で行われます。

推定量を用いた帰無仮説$H_0$ (対立仮説 $H_1 $ )を立てる
有意水準$\alpha $ を決め、棄却域 $ \Theta _{c} $ を定める
統計量$ \theta $を計算し、棄却域に入っているか調べる
棄却域に入っていれば、帰無仮説を否定して、対立仮説を採用する

最後に、簡単な例を書いて終わりにします。

統計的仮説検定の例

定番の検定を挙げておきます。

[平均値を比べる検定]
t検定と呼ばれる手法です。詳しい計算は、t分布の記事を読んでください。
分散が等しい2種類の正規分布から得られたデータがあるとします。
$X_1 , \cdots , X_m \sim \mathcal{N} (\mu _1,\sigma ^2 ), Y_1 , \cdots ,Y_n \sim \mathcal{N} (\mu _2 , \sigma ^2 ) $です。
帰無仮説を$ \mu _1 = \mu _2 $とします。
このとき、/( \mu _1 = \mu _2 \)だとすると、t分布に従う量が計算出来ます。
$$\begin{eqnarray}
T&=& \frac{ (\bar{X} -\bar{Y} )\sqrt{mn} /( \sigma \sqrt{m+n} )} { \sqrt{ \hat{\sigma ^2 } / \sigma ^2 }}\sim t_{m+n-2}
\end{eqnarray}$$
T,t分布, 有意水準$ \alpha $を決める事で、統計的仮説検定を行えます。
上で考えた例のように、
$$\begin{eqnarray}
P(T>t_{m+n-2 ,\alpha /2 }) =\alpha /2
\end{eqnarray}$$
を満たすように $ t_{m+n-2 ,\alpha /2 } $を決めて¹¹、おけば、棄却域は、
$$\begin{eqnarray}
\Theta _c =\{ X,Y| |\bar{X} – \bar{Y}\sqrt{mn} /\sqrt{m+n} > t_{m+n-2 , \alpha /2 } \}
\end{eqnarray}$$
となります。

[分散を比べる検定]
F検定と呼ばれる検定です。詳しい計算は、F分布の記事を読んでください。
2種類の正規分布から得られたデータがあるとします。
$X_1 , \cdots , X_m \sim \mathcal{N} (\mu _1,\sigma _1 ^2 ), Y_1 , \cdots ,Y_n \sim \mathcal{N} (\mu _2 , \sigma _2 ^2 ) $です。
帰無仮説を$ \sigma _1 =\sigma _2 $と置きます。
このとき、$ \sigma _1 = \sigma _2 $だとすると、F分布に従う量が計算出来ます。
分散を不偏分散で推定します。
$$\begin{eqnarray}
\hat{\sigma _1 } ^2 &=& \sum \frac{( X_i – \bar{X} )^2}{m-1} \\
\hat{\sigma _2 } ^2 &=& \sum \frac{( Y_i – \bar{Y} )^2}{n-1}
\end{eqnarray}$$
仮に、$ \sigma _1 = \sigma _2 =\sigma $だとすると、
$$\begin{eqnarray}
\hat{\sigma _1 } ^2 / \hat{\sigma _2 }^2 \sim F_{m-1 , n-1}
\end{eqnarray}$$
で、F分布が出て来ます。
上と同じように、$ F_{m-1, n-1, \alpha /2 } $を定めると、棄却域が
$$\begin{eqnarray}
\Theta _c =\{ X,Y| \hat{\sigma _1 } ^2 / \hat{\sigma _2 }^2 > F_{m-1, n-1, \alpha /2 } または \hat{\sigma _1 } ^2 / \hat{\sigma _2 }^2 > F_{m-1, n-1, 1-\alpha /2 } \}
\end{eqnarray}$$
と求められます。

まとめ

統計的仮説検定のモチベーションをあげた
統計的仮説検定の原理を説明した
有意水準について説明した
統計的仮説検定の手順を説明した
例を挙げた

施策を打ち出す前後でのブログのアクセス数や、種類ごと商品の売り上げ、色々な条件で試作した製品の性能など、なんでも良いです。
状況に依るんですが。
データを扱うという事はそういう事な気がしますが。
その場合は$ \mu _1 < \mu _2 $が帰無仮説です。
$ \mu > 0 $ を対立仮説にする時の$ \Theta _0 , \Theta _0 ^c $を考えてみてください。
$ \Theta _0 ^c $を少し狭めたような集合$ \Theta _c $を作って、そこに$ \theta $が入っていれば、帰無仮説を否定するという事です。
有意水準は慣習的に0.01 か0.05を使います。
具体的な計算をするには何らかの確率分布が必要です。普通は2種類データがあったら2つ確率分布を用意しますが、今回は楽をするために一つにします。
計算が謎の人は、正規分布についての記事を読むのをお勧めします。
教科書やライブラリに数字が入ってるので、手計算する事はありません。
教科書に、t分布表が載っていますし、python でも計算できるので、手計算する事はないです。