ベイズ統計学でブログのアクセス数を解析する

ブログを始めて4か月くらい経ちました。¹ 最初の1週間はTwitterでフォローしてくれた人が見るだけと言うサイトでしたが、現在は検索エンジンから殆どのユーザーがブログを見てくれています。
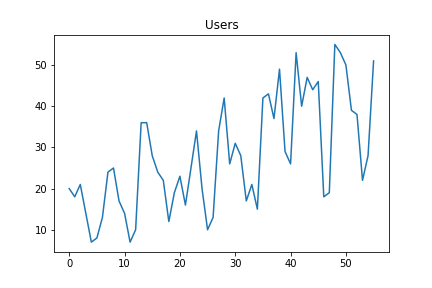
なんとなく、あるタイミングからアクセス数が増えたな～という感覚があります。機械学習系の手法で、増えた”タイミング”を検出できないでしょうか?²2019年10月1日からのユーザー数は以下のグラフのように変動しています。

このブログには、ポアソン混合モデルの記事があります。そして、python で実装してみた記事もあります。
アクセス数は0以上の整数で、実感としてある時を境にアクセス数が変化したと感じています。ポアソン分布を2つ用意して、ある時点からアクセス数が変化したと仮定すれば、ポアソン混合モデル³ の変分推論で、アクセス数が変化したタイミングを捕まえる事が出来ます。
元ネタはネットサーフィンしてた時に見つけました。緑本⁴ の作者のサイトです。

モデルの作成
更新式の導出
python による実装
まとめ

モデルの作成

今回使うモデルを書き下しましょう。本家に倣って、アクセス数を表す変数は$ c $、欲しいタイミングは$\tau $、データ数に関する添え字は$n $ で表します。また、ポアソン分布のパラメーター$ \lambda _1 , \lambda _2 $はそれぞれガンマ分布に従うとします。
$$\begin{eqnarray}
p( C, \tau , \lambda _1 , \lambda _2 ) &=& p(C| \tau , \lambda _1 , \lambda _2 ) p(\tau ) p(\lambda _1 ) p( \lambda _2 ) \\
p(C| \tau , \lambda _1 , \lambda _2 ) &=&
\prod_{n=1} ^{N} { \rm Poi } (c_n |\lambda _1 ) ^{\delta ( n < \tau ) } { \rm Poi } (c_n |\lambda _2 ) ^{\delta ( n \geq \tau ) } \\
p ( \tau ) &=& \frac{1}{N} \\
p(\lambda _i ) &=& {\rm Gam } (\lambda _i | a_i , b_i )
\end{eqnarray}$$
ただし、命題Pに対して $ \delta (P) $で、Pが真のとき1 , Pが偽のとき0を表す関数とします。⁵
ガンマ分布やポアソン分布は以下の式です。⁶
$$\begin{eqnarray}
{ \rm Gam } (\lambda | a,b ) &=& C_{G}(a, b ) \lambda ^{a-1} \exp(-b\lambda )\\
C_G (a,b) &=& \frac{b^a}{\Gamma (a)} \\
{\rm Poi} (c|\lambda ) &=& \frac{\lambda ^{c}}{c!}e^{-\lambda}
\end{eqnarray}$$
隠れ変数たち$ \{ \tau, \lambda _1 , \lambda _2 \} $ は、平均場近似しておきます。
$$\begin{eqnarray}
p(\tau, \lambda _1 , \lambda _2 |C ) = q(\tau ) q(\lambda _1 ) q( \lambda _2 )
\end{eqnarray}$$

変分推論によると、以下の更新式によってパラメーターを更新していけば、データを近似する確率分布が得られます。
$$\begin{eqnarray}
E_{i\neq j}[\log p(X, Z )] &=& \int \log p(X,Z) \prod_{i\neq j} q_i dz_i \\
q^{\ast}_j (z_j) &=& \frac{\exp( E_{i\neq j} [\log p(X, Z)] )}{ \int \exp( E_{i\neq j} [\log p (X, Z)] ) dz_j }
\end{eqnarray}$$
今回の場合だと、$ X=C=\{ c_1 , \cdots , c_N \}, Z=\{Z_1 , Z_2 , Z_3 \} = \{ \tau, \lambda _1 , \lambda _2 \} $です。

更新式の導出

パラメーターの更新に必要な計算を載せます。
$$\begin{eqnarray}
\log q (\lambda _1 ) &=& E_{\lambda _2 } [E_{\tau } [ \log p(C, \tau , \lambda _1 , \lambda _2 ) ]]\\
& \propto & E_{\tau } [ p(C| \tau , \lambda _1 ,\lambda _2 ) ] +\log p(\lambda _1 ) \\
\log q (\tau ) &=& E_{\lambda 1} [ E_{\lambda 2 }[ \log p(C, \tau , \lambda _1 , \lambda _2 ) ]]\\
&\propto & E_{\lambda 1} [ E_{\lambda 2 }[ \log p(C,|\tau , \lambda _1 , \lambda _2 ) ]]
\end{eqnarray}$$
期待値以外を計算して、確率分布の形を決定します。
$$\begin{eqnarray}
\log q (\lambda _1 )
& \propto & \left( \sum_{n} ^{\tau -1} E_{\tau } [ \delta (n< \tau ) ] c_n + a_1 -1 \right) \log \lambda _1 \\
&-& \left( \sum_{n} ^{\tau -1} E_{\tau } [ \delta (n< \tau ) ] +b \right) \lambda _1 \\
\log q (\tau )
&\propto &
\sum_{n=1} ^{\tau -1} ( c_n E_{\lambda _1} [ \log \lambda _1 ] – E_{\lambda _1}[ \lambda _1 ] )
+ \sum_{n=\tau } ^{N} ( c_n E_{\lambda _2} [ \log \lambda _2 ] – E_{\lambda _2} \lambda _2 ] )
\end{eqnarray}$$
$ \log q(\tau) $の計算では、 $ \delta (\tau <n ) $が $ \tau = n, \cdots , N $ で0になることを使いました。$ \log $ を取った部分の計算から、パラメーターを更新した後の確率分布がガンマ分布やカテゴリー分布になることが分かります。
$$\begin{eqnarray}
q (\lambda _i ) &=& { \rm Gam} (\lambda _i |\hat{a_i} , \hat{b_i} )\\
\hat{a_i} &=& \sum c_n E_{\tau } [\delta ( n < \tau ) ] +a_i \\
\hat{b_i} &=& \sum E_{\tau } [\delta ( n \geq \tau ) ] +b_i \\
q (\tau ) &=& \hat{ \pi _{\tau } } \\
\hat{ \pi _{\tau } } &\propto & \exp \left\{ \sum_{n=1} ^{\tau -1} ( c_n E_{\lambda _1} [ \log \lambda _1 ] – E_{\lambda _1}[ \lambda _1 ] )
+ \sum_{n=\tau } ^{N} ( c_n E_{\lambda _2} [ \log \lambda _2 ] – E_{\lambda _2} \lambda _2 ] ) \right\}
\end{eqnarray}$$
⁷ 計算していない期待値は、以下のようになります。$ \psi (x ) $はディガンマ関数です。
$$\begin{eqnarray}
E_{\lambda _i } [\lambda _i ]&=& \hat{a_i} / \hat{b_i} \\
E_{\lambda _i } [\log \lambda _i ] &=& \psi(\hat{a_i} ) – \log \hat{b_i} \\
E_{\tau } [ \delta (n< \tau ) ] &=& \sum_{\tau = n+1} ^{N} \hat{\pi_{\tau} }\\
E_{\tau } [ \delta (n \geq \tau ) ] &=& \sum_{\tau = 1} ^{n} \hat{\pi_{\tau} }
\end{eqnarray}$$
$E_{\tau } [\delta ( n< \tau ) ] = \sum_{\tau=1} ^{N} \hat{\pi_{\tau}} \delta ( n< \tau ) $に注意しましょう。$ \tau $について期待値を取る時は “n”が定数です。
混合ポアソンモデルの時と同じような結果が出てきました。pythonでこの計算を実装して、ブログのユーザー数が変化したタイミングを予測してしましょう。

python による実装

記事で使っているソースコードはgithub に置いてあります。
https://github.com/msamunetogetoge

変分推論の記事と殆ど同じですが、変分推論を行うクラスを写しておきます。


class VI():
    def __init__(self,x,a,b,pi):
        self.x=x
        self.a = a
        self.b =b
        self.N = len(self.x)
        self.pi = np.zeros(self.N)
        self.Tau =np.array([])

    def Estep(self):
        self.E_lam = self.a/self.b
        self.E_loglam = psi(self.a) -np.log(self.b)
        log_pi = np.zeros(self.N)
        for i in range(self.N):
            log_pi[i] =  np.sum(self.x[:i] *self.E_loglam[0]  - self.E_lam[0] ) 
            + np.sum(self.x[i:]*self.E_loglam[1] - self.E_lam[1]  )
        
        log_pi-= np.max(log_pi)
        self.pi = np.exp(log_pi)
        self.pi /= np.sum(self.pi)    
        
        return  self.pi

    def Mstep( self):
        self.pi =self.Estep()
        self.E_d = np.zeros((2,self.N))
        for i in range(self.N):  
            self.E_d[0,i] = np.sum(pi[i+1:])
            self.E_d[1,i] = np.sum(pi[:i+1])

        a_hat =np.dot(self.x, self.E_d.T ) + self.a
        b_hat = np.sum(self.E_d, axis=1) +self.b

        return  a_hat , b_hat

    
    def itr_calc(self,max_itr ):
        
        for i in range(max_itr):
            self.a,self.b = self.Mstep()
            self.pi = self.Estep()
            tau = np.argmax(self.pi)
            self.Tau =np.append(self.Tau,tau)
        
        E_x =np.zeros(self.N)
        for i in range( self.N):
            if i< tau:
                E_x[i] = (self.a/self.b)[0]
            else :
                E_x[i] = (self.a/self.b)[1]     
        return self.pi, E_x

$E_x $に $ \tau $ の期待値を格納しています。
計算させてみましょう。for 文を使ってるので(?)計算が遅いのです。max_itr = 10くらいでやっても同じような結果になります。

a=np.abs(np.random.randn(2))
b=5*np.abs(np.random.randn(2))
pi = (1/len(x))*np.ones(len(x))
cal = VI(x=x, a=a, b=b, pi =pi )


pi, E = cal.itr_calc( max_itr= 100)

日ごとのユーザー数と期待値を重ねて描いてみます。

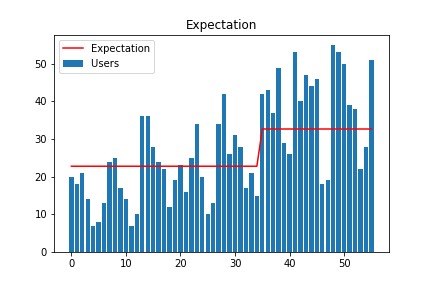
事後分布がどうなっているか見てみましょう。

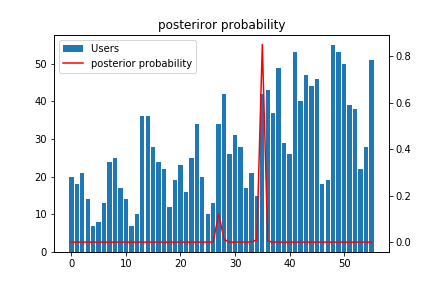
山が2つありますが、後半からユーザーが増えたと判断しているようです。
ぱっと見では後半の方が正しい判断をしている雰囲気を感じます。機械学習の手法としてベイズを使うと、モデルが出した答えの確からしさが自動的に付いてくるので良い感じです。
ちなみに、変化前後での$ \lambda $をコード内の cal.a / cal.b で見ると、23 , 33となっていました。
また、$ \tau = 35 $となっている⁸ので、 11月5日が変化点に当たります。その付近に良い感じの記事があれば、正解と言う感じです。
新しく出したわけでは無いですが、勾配消失や、勾配爆発に関する記事を11/2に更新しています。
勾配消失の様子をtensorboard で可視化したのを追記したのが良かったらしく、結構読まれています。(当ブログ比)